La vida social de los routers. Aplicando el conocimiento de las redes humanas al diseño de las redes de ordenadores [1]

Valdis Krebs[2] - Orgnet

Resumen

El diseño de redes de ordenadores debe tener en cuenta cómo están interconectados los routers[3] y los circuitos en un sistema global, conformando una estructura resistente. El análisis de redes sociales puede aplicarse en el diseño de las redes de ordenadores. Concretamente, en este artículo se utilizan los indicadores de centralidad para analizar la eficiencia y la resistencia de las redes de ordenadores.

Palabras clave: Redes de ordenadores – Redes humanas – Centralidad –  Eficiencia – Resistencia.

Abstract

Network design must carefully consider how routers and circuits are interconnected to form an overall system with as few single points of failure as possible. Social network analysis can be applied to the design of computer networks. In this paper the centrality measures are used to analyse the efficiency and the resiliency of computer networks.

Key words: Computer networks – Human networks – Centrality – Eficiencia – Resiliency.

Con frecuencia olvidamos que las redes de ordenadores se instalan para  hacer de soporte a las redes humanas –es decir, a los intercambios persona-a-persona de información, conocimiento, ideas, intuiciones y consejos. Este artículo recurre a la tecnología que fue desarrollada para medir y hacer mapas de redes humanas –el análisis de redes sociales- y aplica algunos de sus principios y algoritmos en el diseño de redes de ordenadores. Cuando vemos cada vez más modelos peer-to-peer (P2P) de redes de ordenadores, la métrica P2P resulta cada vez más aplicable al análisis de redes humanas[4].

Los analistas de redes sociales ven los sistemas humanos complejos como un sistema interconectado de nodos (personas y grupos) y lazos (relaciones y flujos) –igual que las inter-redes de routers y enlaces. Las redes humanas son con frecuencia sistemas emergentes, no planificados. Su crecimiento es esporádico y auto-organizado (Krebs, 1996). Los lazos de las redes se distribuyen irregularmente, con una alta densidad de lazos en algunas áreas de la red, mientras que otras están escasamente conectadas. Se les denomina “redes de mundo pequeño” (Watts & Strogatz, 1998). Las redes de ordenadores tienen con frecuencia unos patrones de conexión similares –una densa interconectividad entre subredes, con conexiones más escasas que unen las subredes en una inter-red más amplia.

Los consultores e investigadores se centran en los geodésicos –los caminos más cortos en la red. Muchos de los algoritmos de redes sociales actuales se basan en una rama de las matemáticas denomina teoría de grafos. Los científicos de redes sociales han centrado su trabajo, y en consecuencia sus algoritmos, en las siguientes áreas:

• Centralidad de un nodo individual en una red más amplia –dependencia de la red y carga de un router individual.
• Distribución de caminos global –buena conectividad sin demasiadas tablas de enrutamiento.
• Mejora del flujo de comunicación entre grupos –diseño de mejores topologías.
• Patrones de redes en torno a ego-redes –estrategias para analizar y manipular las conexiones de un router individual.
• Análisis del comportamiento del flujo de información de una organización cliente –cómo las redes de ordenadores pueden soportar redes humanas.

Uno de los métodos utilizados para comprender las redes y sus participantes es evaluar la localización de los actores en una red. Medir la localización de una red es encontrar la centralidad de un nodo (Freeman, 1979). Todas las medidas de redes que discutimos aquí se basan en geodésicos –el camino más corto entre dos nodos cualesquiera. Veamos una red social denominada “red cometa”, que muestra de un modo efectivo la diferencia entre los tres indicadores de centralidad más populares –el ABC- actividad (Activity), intermediación (Betweenness) y cercanía (Closeness). Este modelo fue desarrollado por David Krackhardt (1990), un líder en los estudios de redes sociales.

Actividad

La Figura 1 muestra una red social simple. Un lazo entre un par de nodos representa un flujo bidireccional de información, o el intercambio de conocimiento entre dos individuos. Los investigadores de redes sociales miden la actividad de un nodo utilizando el concepto de grado (degree) –el número de conexiones directas que tiene un nodo.

En esta red humana, Diane tiene el mayor número de conexiones directas, lo que la convierte en el nodo más activo en la red con la puntuación de grado más alta. El sentido común dicta que en las redes personales “mientras más conexiones, mejor”. Pero este no es siempre el caso. Lo que realmente importa es a donde conducen dichas conexiones -¡y cómo conectan a los que de otro modo estarían desconectados! (Burt, 1992). En este caso Diana sólo tiene conexiones con otros de su cluster más inmediato. Ella sólo conecta a aquellos que ya están conectados entre sí -¿tiene demasiados vínculos redundantes?

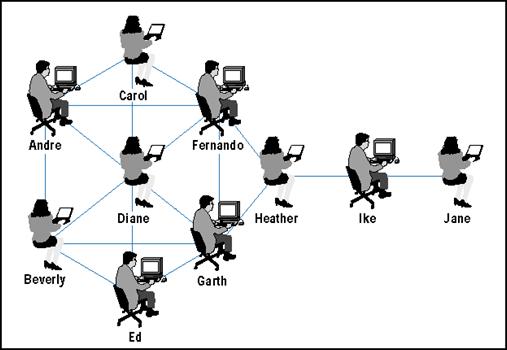
Figura 1. Red humana

Intermediación (Betweenness)

Mientras que Diane tiene muchos vínculos directos, Heather tiene pocas conexiones directas –estando por debajo del promedio en la red. No obstante, en cierto sentido, ella tiene una de las mejores ubicaciones en la red –es una puerta fronteriza y ejerce el rol de broker. Está entre dos componentes importantes, con un papel similar al de un router de frontera. La buena noticia es que juega un papel importante en la red, la mala noticia es que se trata de un punto de quiebra. Sin ella, Ike y Jane se separarían de la información y el conocimiento del cluster de Diane.

Cercanía (Closeness)

Fernando y Garth tienen menos conexiones que Diane. Sin embargo, el patrón de sus lazos les permite acceder a todos los nodos en la red más rápidamente que ningún otro. Tienen el camino más corto hacia todos los demás –están cerca de todos y cada uno. Aumentar la cercanía entre todos los routers mejora la actualización y reduce la cantidad de saltos. No obstante, aumentar la cercanía de sólo uno o de unos pocos routers ocasiona resultados contraproducentes, como veremos más adelante.

Sus posiciones demuestran que cuando se trata de conexiones en una red, la calidad es mejor que la cantidad. Situación, situación, situación –la regla de oro de la inmobiliaria también funciona en las redes. Cuando hablamos de vivienda es la geografía –tu barrio físico. En las redes, se trata de tu ubicación virtual determinada por tus conexiones –tu vecindario relacional.

Centralización de la red

La centralidad de los individuos en una red da una idea de la ubicación de los individuos en la red. La relación entre las centralidades de todos los nodos puede revelar mucho sobre la estructura global de la red. Una red muy centralizada es aquella que está dominada por uno o varios nodos muy centrales. Si estos nodos son dañados o eliminados, la red se fragmenta rápidamente en subredes desconectadas. Los nodos altamente centrales pueden convertirse en puntos críticos de fallo de un sistema. Una red con una baja centralización no está dominada por uno o varios nodos –y dicha red no tiene puntos únicos de fallo. Es resistente en presencia de muchos fallos locales. Muchos nodos o enlaces pueden fallar, a la vez que permite que los nodos restantes sean alcanzados a través de nuevos caminos.

Longitud de camino promedio en una red

Mientras más corto es el camino, menos saltos o pasos son necesarios para ir de un nodo a otro. En las redes humanas, los caminos más cortos implican una comunicación más rápida con menos distorsión. En las redes de ordenadores, la degradación y la demora de la señal no son un problema. No obstante, una red con muchos caminos cortos conectando a todos los nodos será más eficiente en la transmisión de datos y en la re-configuración después de un cambio topológico.

La longitud de camino promedio correlaciona fuertemente con la Cercanía de la red. Cuando la cercanía de todos los nodos entre sí mejora (cercanía promedio), la longitud del camino promedio en la red también mejora.

Topología inter-red

En un libro reciente sobre diseño de redes, Advanced IP Network Design (Retana, Slice & White, 1999), los autores definen una topología bien diseñada como la base de una red estable y de buen comportamiento. Además proponen que “tres metas que compiten entre sí deben ser equilibradas para el buen diseño de una red”:

• Reducción del número de saltos.
• Reducción de los caminos disponibles.
• Aumento del número de fallos que la red puede resistir.
• Nuestros algoritmos de redes sociales pueden ayudar en la medición y la consecución de las tres metas.
• Reducir el número de saltos implica minimizar la longitud del camino promedio por toda la red –maximizar la cercanía de todos los nodos entre sí.
• Reducir los caminos disponibles lleva a minimizar el número de geodésicos por toda la red.
• Aumentar el número de fallos que una red puede resistir se centra en minimizar la centralización de la red completa.

En las siguientes páginas examinamos varias topologías de redes y las evaluamos utilizando indicadores de redes sociales, mientras recordamos estas tres metas competitivas en el diseño de redes.

Los modelos que examinamos no incluyen a las estructuras jerárquicas –con controladores del Núcleo, la Distribución y el Acceso- que se encuentran en las redes de cientos o miles de routers. Examinamos topologías planas, no jerárquicas, tales como las que se encuentran en las inter-redes más pequeñas, las subredes de área, o en backbones[5] centrales. Las topologías que modelamos son las más comúnmente utilizadas –la de estrella, la de anillo, la de malla completa y la de malla parcial. Calculamos las medidas de redes sociales en cada una de estas tipologías, y discutimos cómo los diferentes indicadores nos ayudan a conseguir las metas competitivas señaladas más arriba.

Topología de estrella

La topología de estrella, mostrada en la Figura 2, tiene muchas ventajas –pero un defecto deslumbrante. Las ventajas incluyen la facilidad de gestión y de configuración para los administradores de la red. Para la estrella, las tres metas competitivas quedan del siguiente modo:

• Reducción del número de saltos: La pequeña longitud de camino promedio en la red (1.75) cubre bien esta meta. Cualquier router puede alcanzar a cualquier otro en dos o menos pasos.
• Reducción de los caminos disponibles: El hecho de que haya un número mínimo de posibles caminos disponibles (56) para alcanzar todos los demás nodos, hará que no se sobrecarguen las tablas de enrutamiento ni se originen demoras en la actualización de las mismas. Sólo son necesarios siete enlaces bidireccionales para crear los caminos disponibles.
• Reducción de los fallos de la red: La red falla lastimosamente si el router A se cae. Además, cualquier fallo en un enlace aísla al router asociado. No hay múltiples caminos para llegar a cada router.

El router A no es sólo un punto crítico de fallo, sino que es también potencialmente un cuello de botella. Muy probablemente se sobrecargará con el flujo de paquetes y las actualizaciones de enrutamiento a medida que se añadan más routers en la estructura de estrella. El router A obtiene la puntuación más alta en Actividad, Intermediación y Centralidad (1.000). Como resultado, la red está muy centralizada en torno al router A desde la perspectiva de los tres indicadores.

 

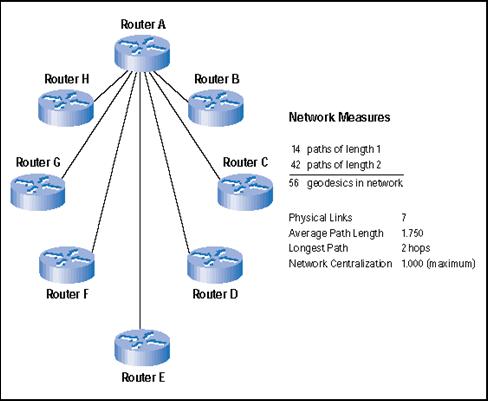
Figura 2. Routers en una tipología de estrella

Leyenda: Medidas de redes. 14 Caminos de longitud 1 + 42 caminos de longitud 2 = 56 geódesios en la red. Enlaces físicos: 7; Longitud de camino promedio: 1,750; Camino más largo: 2 saltos; Centralización de la red: 1.00 (máximo).

Topología de anillo

La topología de anillo, mostrada en la Figura 3, es una mejora sobre la estrella. Tiene algunas de las mismas ventajas, pero no elimina todos los inconvenientes de la estrella. Las ventajas incluyen la facilitad de gestión y de configuración para los administradores de la red –puesto que añadir otro router es muy simple. A diferencia de la topología de estrella, el anillo proporciona cierta redundancia y, por tanto, elimina el punto crítico de fallo: todos los nodos tienen un camino alternativo a través del cual pueden ser alcanzados. No obstante, todavía es vulnerable tanto a los fallos de los enlaces como a los de los routers. Para el anillo, las tres metas competitivas quedan como sigue:

• Reducción del número de saltos: Una longitud de camino promedio de 2.5 es bastante larga para una red pequeña de ocho nodos. ¡Algunos routers (concretamente, A y E) requieren de cuatro pasos para alcanzarse el uno al otro! Muchos controladores físicos de anillo ocultan esta complejidad desde los controladores de IP para hacer que estos saltos sean invisibles a los protocolos de enrutamiento.
• Reducción de los caminos disponibles: Esta configuración tiene más geodésicos (64) que la estrella, aunque no de un modo significativo como para sobrecargar las tablas de enrutamiento ni causar demoras durante su actualización.
• Reducción de los fallos de la red: Incluso aunque la centralización de la red está al mínimo (ningún nodo es más central que otro), esta red llega al fallo rápidamente debido a su débil redundancia. La topología de anillo puede soportar el fallo de un enlace o de un router y mantener todavía una red contigua. Pero dos fallos simultáneos pueden dar lugar a que haya segmentos inalcanzables debido a su falta de redundancia.

La mayoría de las tecnologías modernas de anillo, tales como la red óptica sincrónica (Synchronous Optical Network, SONET) o el protocolo de transporte de paquetes dinámico de Cisco (Cisco Dynamic Packet Transport Protocol, DPT), añaden una medida de redundancia poniendo en funcionamiento un anillo doble que se repara a sí mismo si se corta un enlace. La red se “cierra” para evitar la línea que se ha caído y opera a una menor velocidad. Un camino de dos saltos puede convertirse en un camino de seis saltos con que sólo falle un enlace. Esto puede originar la congestión de la red si el anillo doble original estuviese siendo utilizado para datos en todas las direcciones.

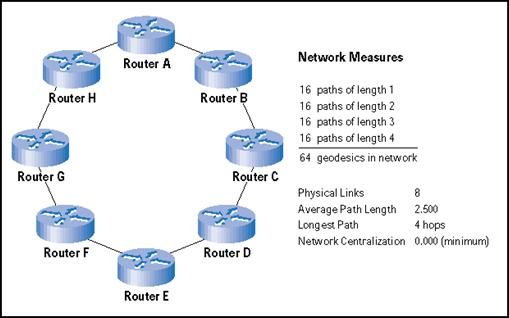
Figura 3. Routers en una topología de anillo

Leyenda: Medidas de redes. 16 Caminos de longitud 1 + 16 caminos de longitud 2 + 16 caminos de longitud 3 + 16 caminos de longitud 4 = 64 geódesios en la red. Enlaces físicos: 8; Longitud de camino promedio: 2,500; Camino más largo: 4 saltos; Centralización de la red: 0.000 (mínimo).

Topología de malla completa

La topología de malla completa tiene varias grandes ventajas y varios defectos. Las ventajas incluyen una longitud de camino corta (un salto) hacia todos los demás routers, y máxima resistencia al fallo si los enlaces o los routers empiezan a fallar. Las desventajas giran en torno a la complejidad creada por esta tipología. Para la malla completa, las tres metas competitivas quedan como sigue:

• Reducción del número de saltos: La longitud de camino más corta posible se consigue en todas las rutas. Todos los nodos pueden alcanzarse entre sí en un salto.
• Reducción de los caminos disponibles: Hay un número mínimo de caminos disponibles posibles (56) para alcanzar todos los demás nodos. Las entradas no sobrecargarán las tablas de enrutamiento, ni causarán demoras durante la actualización de las mismas.
• Reducción de los fallos de la red: La red no depende de ningún nodo (centralización de la red = 0.000). Esta configuración representa la topología más robusta disponible. Son muy pequeñas las probabilidades de que ocurran en el mismo periodo de tiempo el número de fallos necesarios para que la red se fragmente.

Todas las desventajas de la topología de malla completa se centran en un defecto deslumbrante: hay demasiados enlaces físicos. Si los routers están muy lejanos, los costes de los enlaces pueden convertirse rápidamente en prohibitivamente caros puesto que añadir routers crea una explosión geométrica en el número de enlaces que se requieren. Pronto los routers no tienen suficientes puertos para soportar esta tipología. La administración del sistema y mantener un mapa actualizado de la topología se hace cada vez más complejo, a medida que se añaden nuevos routers. La red de la Figura 4 tiene 28 enlaces de doble sentido. Si se duplican los routers, en una topología de malla completa, el número de enlaces aumenta en un factor mayor de 4.

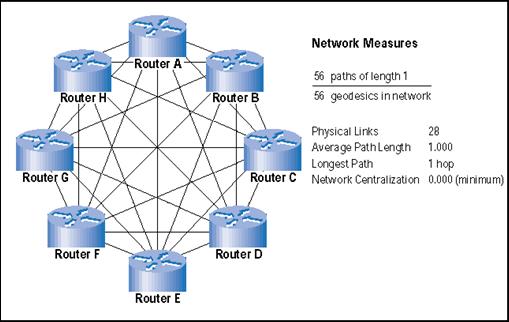
Figura 4. Routers en una topología de malla completa

Leyenda: Medidas de redes. 56 Caminos de longitud 1 = 56 geódesios en la red. Enlaces físicos: 28; Longitud de camino promedio: 1,000; Camino más largo: 1 salto; Centralización de la red: 0.000 (mínimo).

Topología de malla parcial

La topología de malla parcial es bastante diferente. Es la más difícil de construir. No hay una regla simple a seguir, a diferencia de los casos anteriores (regla para la estrella: conecta a todos al router A; regla para la malla completa: conecta todos con todos). Si se construye incorrectamente, la disposición de malla parcial puede tener muchas de las desventajas de las topologías anteriores sin tener muchos de sus beneficios. Si se construye correctamente, la verdad es la contraria: más ventajas y menos desventajas.

Construir una topología de malla parcial exitosa es donde realmente entra en juego el uso interactivo de nuestros indicadores de redes sociales. El diseño de más abajo surgió después de varias iteraciones. Con cada iteración la longitud del camino promedio fue cayendo hasta que pareció alcanzar un umbral donde ningún otro cambio disminuía el número de saltos sin aumentar significativamente el número de enlaces físicos necesarios. Para la malla parcial, las tres metas competitivas quedan como sigue:

• Reducción del número de saltos: La pequeña longitud del camino promedio en la red (1.667) cubre bien esta meta. Cada router puede alcanzar a cualquier otro en dos o menos pasos. La longitud del camino es menor que en los casos de las topologías de estrella y de anillo.
• Reducción de los caminos disponibles: El número de caminos disponibles en la red (72) es el mayor de todas las topologías, aunque no significativamente mayor que la de anillo. A medida que el número de nodos en una red aumenta, esto podría convertirse en un problema. El compromiso entre la longitud del camino promedio y el número de caminos requiere de una fina monitorización.
• Reducción de los fallos de la red: La centralización de la red (0.000) es la misma que para la topología de malla completa. Ningún router ni enlace es más importante que otro. Esta red no se fragmenta rápidamente cuando se eliminan nodos o enlaces. Son pequeñas las probabilidades de que ocurran en el mismo periodo de tiempo el número de fallos necesarios para que se fragmente la red. Aunque nosotros optimizamos la centralización para esta pequeña red “de juguete”, no podemos esperar esto mismo para la mayoría de las redes reales. No obstante, la meta sigue siendo mantener esta métrica tan pequeña como sea posible.

La topología de la Figura 5 fue construida tomando como punto de partida una topología de anillo –una arquitectura simple. Se añadió un enlace y volvimos a medir la red. ¿Era esta estructura mejor que la anterior? En caso de ser así, se mantenía la estructura actual y se añadía un nuevo enlace para volver a medir la red. Este proceso iterativo se mantuvo hasta que no se consiguieron posteriores mejoras después de varios cambios. El proceso no garantiza una solución óptima, pero rápidamente consigue una buena solución: incluso redes amplias mejoran rápidamente con el añadido de unos pocos enlaces.

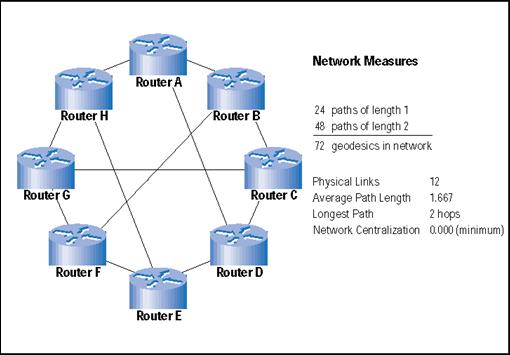
Figura 5. Routers en una topología de malla parcial

Leyenda: Medidas de redes. 24 Caminos de longitud 1 + 48 caminos de longitud 2 = 72 geódesios en la red. Enlaces físicos: 12; Longitud de camino promedio: 1,667; Camino más largo: 2 saltos; Centralización de la red: 0.000 (mínimo).

Una rareza de las redes es que a veces puedes restar sumando: añades un enlace a una red y se reduce la longitud del camino promedio. Lo contrario también ocurre a veces. Puedes sumar restando: eliminas un lazo y se observa el crecimiento del número de saltos promedio. En cualquier caso, nunca se tiene la certidumbre de qué efecto tendrá el añadido o la eliminación de un lazo. Nunca es un fenómeno lineal ni local. El tamaño y la dirección de estos cambios dependen de la topología previa de la red y de la ubicación del lazo que se elimina o se añade. Es clave disponer de un modelo que permita rápidos cálculos del tipo “qué pasa si…”.

Experimentemos con la eliminación de lazos de modo aleatorio (una situación similar al fallo de enlaces entre routers). Si eliminamos el enlace entre el router A y el router H en la Figura 5, el número de geodésicos en la red aumenta de 72 a 76, y la longitud de camino promedio aumenta hasta 1.815. Sin embargo, eliminando un lazo diferente, el que hay entre G y F, se reduce el número de geodésicos en la red de 72 a 66, mientras que la longitud del camino promedio aumenta sólo hasta 1.727. Si estamos preocupados sobre la existencia de demasiados caminos en la red, podemos eliminar otro lazo, el que hay entre B y C. Esto disminuye aún más el número de caminos más cortos hasta 60, mientras que reduce el número de enlaces físicos hasta 10. Esto está muy cerca de los 56 caminos en la muy eficiente topología de estrella. Pero mientras que la estrella es muy vulnerable debido a su punto crítico de fallo, esta malla parcial, con la eliminación de dos enlaces, es todavía robusta. Mientras que el número de geodésicos cae, la longitud de camino promedio asciende suavemente hasta 1.80 con la eliminación del segundo enlace. La Figura 5 no tiene caminos mayores de dos saltos. Con la eliminación de los dos enlaces (de G a F, y de B a C), ahora disponemos de 8 geodésicos de tres saltos, mientras que al mismo tiempo hay 12 geodésicos menos que cargar en las tablas de enrutamiento y dos enlaces físicos menos. Es un equilibrio constante.

Backbone de NSFNET

La red del Backbone de NSFNET, mostrada en la Figura 6, conectó a los centros de super-computación en Estados Unidos en 1989. Es un diseño de malla parcial que funciona como un ejemplo de la vida real con el que probar nuestros algoritmos de redes sociales.

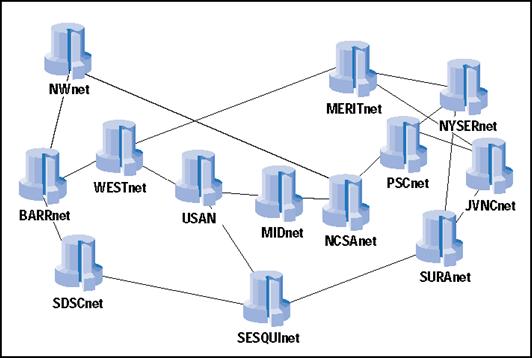
Figura 6. NSFnet en 1989

Recordemos nuestras tres metas competitivas para un buen diseño de inter-redes.

• Reducir el número de saltos: longitud de camino promedio en pasos/saltos.
• Reducir los caminos disponibles: total de geodésicos en la red.
• Aumentar el número de fallos que la red puede soportar: centralización de la red.

¿Qué pasa con estas metas cuando experimentamos fallos en los enlaces o en los nodos de la red? La Tabla 1 muestra la métrica base para la Figura 6, y a continuación muestra qué ocurre con las métricas, y con nuestras tres metas, cuando tienen lugar cinco fallos diferentes.

Tabla 1. Posibles fallos de enlaces y de nodos.

El más dañino fue el fallo del enlace 4, el fallo del lazo entre el NCSA y el PSC. Este enlace corresponde a dos de los nodos más centrales en la red. Si el flujo entre nodos se distribuye de un modo irregular, este enlace es uno de los más transitados en la red.

El menos perjudicial fue el fallo del nodo 3, el JVNC. De hecho, ¡este fallo mejora la mayoría de las métricas! Al eliminar este nodo de la red, el número de caminos de la red disminuye significativamente, la centralización de la red disminuye, la longitud del camino se reduce ligeramente, y el camino más largo es todavía de cuatro saltos.

El diseño de la topología original de la NSFnet es muy eficiente. Intenté dos estrategias diferentes para mejorar la red. La primera estrategia consistió en mover enlaces ya existentes para conectar a diferentes parejas de routers. Pero no encontramos ninguna topología claramente mejor reordenando los enlaces entre routers. No pude encontrar un diseño mejor que redujese tanto el número de geodésicos como la longitud del camino, sin aumentar significativamente al mismo tiempo el número de enlaces físicos en la red.

La segunda estrategia es contra-intuitiva, pese a que con frecuencia las redes responden bien a este enfoque. Es la aproximación de “restar sumando” que describimos más arriba. Añadiendo nuevos enlaces en el lugar apropiado en la red, podemos no sólo reducir la distancia entre nodos, sino también aumentar el número de geodésicos en la red.

Dado que los nodos de la NSFnet tenían un límite máximo de tres vecinos directos, comencé por conectar los nodos de grado 2. Las opciones de 1 a 3 en la Tabla 2 muestran las diversas combinaciones y su efecto en el total de la red. Las mejoras fueron mínimas, si bien cada opción ofrece ventajas específicas. La opción 2 ofrece más mejoras que las otras.

• El geodésico más largo se redujo a tres saltos.
• La longitud de camino promedio se redujo en el conjunto de la red.
• El número de caminos para que recordasen los routers se redujo ligeramente.
• La centralización de la red no aumentó suficientemente como para afectar de modo significativo al número de errores que la red podría soportar.

Tabla 2. Posibles mejoras de la red

Las mejoras en la Opción 2 (enlace añadido: NW-SDSC) fue implementada de hecho en la versión de 1991 de la NSFnet –un excelente ejemplo de la dinámica de red de “restar sumando”. Las redes son sistemas complejos. Cómo responde la red al cambio es algo que se basa en la distribución y los patrones de conexiones a través de la red.

Conclusión

En el mundo real es posible que no tengamos la flexibilidad para experimentar con nuestro modelo de red que hemos tenido en estos ejemplos. Habrá más limitaciones. Los flujos de información en tu organización pueden requerir que pares específicos de routers tengan enlaces directos –incluso aunque dichas conexiones no fuesen recomendables de acuerdo con los algoritmos que hemos estado examinando. No obstante, cuando sabemos qué conexiones “tienen que estar”, podemos experimentar con la ubicación de las demás conexiones utilizando la métrica de las redes sociales para indicar cuándo nos estamos acercando a una topología robusta y eficiente. Dadas determinadas “condiciones iniciales”, los métodos de redes sociales pueden modelar nuestras redes de ordenadores y sugerir cambios en los enlaces[6] para conformar una topología efectiva, que tiene un bajo promedio de saltos, no demasiados caminos y suficiente redundancia.

Bibliografía

Burt, R. S. (1992). Structural Holes--The Social Structure of Competition. Harvard University Press.

Freeman, L. (1979). "Centrality in Social Networks: A Conceptual Clarification", Social Networks, 1, 1979.

Krackhardt, D. (1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations", Administrative Science Quarterly, 35, 351.

Krebs, V. (1996). "Visualizing Human Networks. Release 1.0.", Esther Dyson's Monthly Report, February.

Retana, A., Slice, D., White, R. (1999). Advanced IP Network Design. Cisco Press.

Watts D. & Strogatz S. (1998). "Collective Dynamics of Small World Networks", Nature, 4 June.