Técnicas para el análisis y visualización de interacciones en ambientes virtuales[1]

Pedro A. Willging – Facultad de Ciencias Exactas y Naturales, Universidad Nacional de La Pampa - CONICET [2]

Resumen

Foros asíncronos, listas de correo electrónico, y salas de chat crean ambientes de interacción virtual en los cuales puede ser difícil detectar problemas de comunicación entre los participantes. Quien quiera enseñar por medio de un ambiente en línea, se encuentra con que los actuales sistemas de gestión de aprendizajes no proveen mucha información respecto de la estructura de comunicación del grupo, nivel de participación, y otras características estructurales de la interacción que se da en este medio.

En este trabajo, se exploró el uso de metodología de análisis de redes sociales (ARS) y visualizaciones en espacios en línea. Se muestra de qué modo se pueden crear objetos visuales que representan las intangibles interacciones en línea y se analizó la utilidad de esas imágenes como dispositivos para reconocimiento de patrones.

Se examinó la validez de las técnicas de ARS y visualizaciones como herramientas para que instructores de cursos en línea e investigadores evalúen participación e interacción en foros de discusión. Este estudio mostró que las métricas ARS y la visualización de interacciones son herramientas útiles y potencialmente efectivas para analizar patrones de interacción en línea.

Palabras clave: Interacciones en línea - Ambientes virtuales – Visualizaciones.

Abstract

Asynchronous forums, e-mail lists, and chat rooms create virtuaql environments where it may not be easy to detect communication problemas among the participants. Anyone who wants to teach through an online environment finds that current learning management systems do not provide enough information about the communication structure of the group, level of participation, and other structural characteristics of the interactions that happen in this environment.

In this work, the use of social network analisis methods (SNA) and visualizations for online environments had been explored. The procedures to create the visual objects that represent intangible online interactions are shown and the usefulness of these images as devices for data pattern recognition is analized.

The validity of SNA techniques and visualizations as tools for instructors of online courses and researchers to evaluate participation and interaction in discussion forums was examined. This study showed that SNA metrics and the visualization of interactions are useful and potentially effective tools to analize online interaction patterns.

Key words: Online interactions – Virtual environments – Visualizations.

El uso de foros asíncronos para enseñanza y aprendizaje en línea ha sido ampliamente adoptado por las instituciones que ofrecen programas y cursos en la modalidad a distancia. Tener a los estudiantes comprometidos en esas discusiones en línea es vital por un número de razones: generan aprendizaje colaborativo, incrementan el diálogo constructivo, y proveen oportunidades para socialización. A diferencia de lo que ocurre en las clases presenciales, donde los gestos y las señales visuales y/o verbales le pueden dar al instructor una idea de la motivación y el nivel de interés de sus estudiantes, en el foro de discusión asíncrono (generalmente basado en texto), no es fácil evaluar el nivel de motivación y compromiso de los participantes.

Debido a que es aún un fenómeno reciente, las interacciones en ambientes virtuales no han sido exploradas de manera exhaustiva. Es crítico identificar nuevas metodologías que puedan ser útiles y efectivas en esta área. Hasta el momento, las investigaciones que estudian interacciones en línea han aplicado métodos más tradicionales, como encuestas y análisis de contenidos. Los análisis de texto/contenido requieren mucho tiempo, y a pesar de que pueden proporcionar información más detallada acerca de un participante o una intervención en particular, este tipo de análisis podría ignorar las relaciones entre los participantes ya que se enfoca en el contenido y no en la estructura del diálogo.

Cuando Moreno (1934) dibujó el primer sociograma (bosquejo compuesto de puntos conectados con líneas) probablemente no imaginó que esos gráficos serían el origen de un nuevo modo de estudiar datos sociológicos. Siguiendo el camino de Moreno, el trabajo fundacional de muchos otros científicos de una variedad de disciplinas (Babelas, 1950; Barnes, 1954; Borgatti & Everett, 1992; Harary & Norman, 1953; Krackhardt, 1987; White, 1963) crearon las bases sólidas de la teoría de análisis de redes sociales (ARS).

La teoría de ARS se ha aplicado en investigaciones de áreas muy diversas, como sociología, antropología, economia, educación y psicologia (Paredes, 2007; Souto-Maior Fontes & Eichner, 2004; Teves, Cribos, Martinez, & Sáenz, 2002) y ha probado que sus métodos son útiles y eficientes para el descubrimiento de fenómenos y relaciones desconocidas.

La representación gráfica es una herramienta clave para analizar redes sociales. Trabajos recientes sobre visualización de actividad de redes han hecho evidente el uso práctico de las métricas ARS. Las técnicas ARS junto con herramientas de visualización pueden convertir representaciones nodales y matriciales de patrones de interacción grupal en dispositivos útiles para el escrutinio de foros de discusión en línea. Estos nuevos modos de mirar relaciones y dinámicas de grupo podrían originar modelos alternativos para la evaluación de ambientes virtuales.

El propósito de este estudio fue examinar la validéz de las técnicas de ARS  y visualizaciones como herramientas para que instructores en línea e investigadores puedan evaluar participación e interacción en foros de discusión en línea (asíncronos). Se utilizaron técnicas ARS y software de visualización 3D para examinar características estructurales de discusiones en línea.

Marco Teórico

Comunicación en Espacios Virtuales

La Internet, con todos sus servicios de red (ftp, e-mail, chat, WWW), ha supuesto un agregado revolucionario a las tecnologías disponibles en educación. Las capacidades de la Web para distribuír contenido multimedia la han convertido rápidamente en un espacio para experimentos educativos. Videoconferencia sobre la Web, sistemas integrados de aprendizaje, ambientes para comunicación síncrono y asíncrono son utilizados como herramientas para la enseñanza, en particular para la modalidad conocida como “enseñanza a distancia”, una modalidad que ha crecido exponencialmente en los últimos años (Inglis, Ling, & Joosten, 2002).

Como con cualquier otra tecnología, la Internet y otras herramientas de comunicación tienen limitaciones y crean consecuencias no anticipadas. La carencia de las señales de la comunicación tradicional en la clase en línea puede ser un impedimento para el aprendizaje. Diferencias en el estilo de conversación pueden afectar el modo en que los estudiantes interactúan, reflexionan y aprenden en el aula virtual. El compromiso con las discusiones en línea es vital para generar aprendizaje colaborativo, pero no todos los estudiantes participan con el mismo interés y motivación. Conseguir participación activa en espacios asíncronos puede ser problemático. Investigando factores que favorecen o inhiben la participación de los estudiantes en discusiones asíncronas, se encontró que el entusiasmo y conocimiento del tutor son los factores más importantes para estimular la participación de los alumnos (Oliver & Shaw, 2003).  Anderson, Rourke, Garrison, y Archer (2001) agregan que para mantener el interés y motivación de los estudiantes, el moderador del foro virtual tiene que asumir el rol de promotor de diálogo. Y para que un curso sea efectivo, se deben incluír estrategias de interacción en su diseño. El rol del instructor, ya sea diseñando o conduciendo las actividades de aprendizaje es de central importancia.

Conceptos y Aplicaciones del Análisis de Redes Sociales

Los elementos básicos del ARS son los provistos por la teoría de grafos para caracterizar redes: nodos y arcos. Los nodos en la red pueden ser personas, organizaciones, eventos o lugares. Los arcos representan las relaciones entre los nodos. Esos arcos pueden ser direccionales y mostrar la frecuencia o fortaleza de la relación (Scott, 2000; Wasserman & Faust, 1994). Las relaciones entre los nodos se pueden traducir en notación matricial para luego aplicar un conjunto de medidas derivadas de la teoría de grafos.

Las medidas derivadas de la teoria de ARS incluyen densidad y centralidad. Para un análisis detallado de las mismas y otras medidas consultar Scott (2000) o Hanneman & Riddle (2005).

Los estudios de ARS emplean dos tipos de herramientas: instrumentos visuales y computacionales. Dentro de las herramientas visuales se encuentra MAGE, un software que fue desarrollado originalmente para visualizar moléculas biológicas (Richardson & Richardson, 1992), pero que es útil también para estudiar redes sociales, semánticas y ecológicas (Freeman 2000). Dentro de las herramientas computacionales, dos de las mas populares son UCINET (Borgatti, Everett, & Freeman, 1992) y Pajek (Batagelj & Mrvar, 2003).

Los conceptos y métodos de ARS han colaborado con el avance de varias disciplinas, desde la psicología social, la antropología y las comunicaciones hasta la política y los estudios de organizaciones (Galaskiewicz & Wasserman, 1994). Estos métodos están siendo usados también en nuevas y emergentes metodologías, como el análisis de redes de hiperenlaces (Park, 2003).

Johnson, Palinkas, y Boster (2003) han hecho un uso extensivo de visualización de estructuras de redes sociales para ilustrar y fundamentar sus estudios culturales sobre la evolución de grupos en estaciones de investigación Antárticas. Encontraron que las dinámicas de grupo pueden variar dramáticamente de un grupo a otro aún dentro del mismo ambiente físico y cultural. También hallaron que los roles sociales (formales e informales) tienen efectos en los patrones de interacción y conexión entre los miembros de la red y en última instancia sobre su rendimiento, productividad, moral, y bienestar psicológico.

Otro ejemplo del uso de las métricas ARS para analizar interacciones en línea es provisto por Boudourides, Mavrikakis, y Vasileiadou (2002). Ellos estudiaron el uso del correo electrónico por un grupo de individuos en una lista de correo. Sus datos primarios consistieron de los registros de 1104 correos electrónicos, de los cuales extractaron la siguiente información: fecha de distribución, nombre de quien envió el mensaje, tema del correo electrónico, y contenido del cuerpo del mensaje. En el estudio hicieron dos análisis: temas y género. Las propiedades de la red que fueron calculadas en el estudio fueron: densidad, y centralidades de grado e intermediación.

Aviv, Erlich, Ravid, y Geva (2003) analizaron datos de dos cursos de tres meses de duración en una red de aprendizaje asíncrono usando ARS para estimar roles, contribuciones individuales, y el proceso colaborativo mismo. Ellos afirman que la cohesión, el rol y la distribución del poder controlan los comportamientos y creencias compartidos, y por lo tanto, la construcción del conocimiento. Este supuesto conduce a pensar que diseños diferentes de los grupos de discusión resultarán en diferencias en la estructura de la red, y por lo tanto diferentes fases de pensamiento crítico. Para probar su afirmación analizaron dos grupos de discusión en línea con diseños muy diferentes. Utilizaron datos de dos cursos de la Universidad Abierta de Israel. Los investigadores usaron Cyram Netminer, un software comercial para análisis y visualización de datos para hacer los cálculos ARS. Crearon la matriz de respuestas usando los mensajes que los miembros enviaron, generando un modelo de red valorado y direccional. Realizaron un análisis de cohesión usando el método de cliques y encontraron marcadas diferencias entre las estructuras de los cliques de los dos cursos. El análisis de roles que efectuaron también encontró diferencias entre las dos redes.

Metodología

Muestra y Recolección de Datos

Dos cursos en línea que forman parte de un programa de maestria en la Universidad de Illinois constituyeron los archivos de los foros de discusión empleados en estos cursos. En sus clases, se emplean los sistemas de gestión de aprendizajes (SGA) WebBoard, BlackBoard y Moodle para sus discusiones en línea.

Los datos recolectados en este estudio provienen de tres fuentes: registros de interacciones en línea, cuestionario y entrevista con los instructores. Las interacciones asíncronas en las clases en línea se archivan en el sistema en forma de registros que muestran quién ha subido un mensaje y quién le responde, incluyendo la fecha y hora de envío, la dirección de correo electrónico de quien creó el mensaje, y otros detalles (como título del tema, cuántas veces ha sido leído, el cuerpo del mensaje, etc.). Se extrajo de esos archivos de interacciones asíncronas quién envió el mensaje y quién respondió al mismo. Esta información se recolectó para cada mensaje en el foro en línea. El cuestionario para instructores proveyó datos adicionales para el estudio. Incluyó preguntas sobre la percepción del instructor acerca de los patrones de interacción de la clase. El cuestionario contuvo ítems diseñados para determinar el conocimiento del instructor acerca del nivel de interacción en la clase, la concentración de esta interacción, y la percepción de los roles que los estudiantes jugaron en el curso. Las entrevistas sirvieron para agregar y confirmar o rectificar la información recogida en los cuestionarios y requirió que los instructores reflexionen acerca de su propio rol en la clase en línea.

Procedimiento

Las discusiones en línea archivadas fueron pre-procesadas como archivos de texto con macros de una planilla de cálculo estándar. Los archivos de texto resultantes, con la información estructural del foro fueron convertidos luego (utilizando un programa desarrollado en Perl) a matrices de adyacencia para poder aplicar las métricas ARS con UCINET (el software usado para calcular las medidas  ARS). La Ilustración 1 muestra un esquema de este proceso. Se cambiaron los nombres de los estudiantes e instructores con un código de letra y número para preservar la confidencialidad de los participantes.

Ilustración 1.  Procesamiento de los datos de interacción.

El cuestionario para instructores fue desarrollado por el investigador de este estudio usando la literatura de ARS como guía y fue revisado por cuatro investigadores para chequear y mejorar la validez interna. A los instructores que participaron en el estudio se les pidió que respondieran el cuestionario en presencia del investigador, quien proveyó aclaraciones acerca de las preguntas cuando fue necesario.

Análisis de los Datos

Una vez obtenidas las matrices de adyacencia, se hicieron los cálculos de ARS con UCINET. Se hicieron análisis de densidad, centralidad (grado, cercanía, e intermediación), y cohesión. Las tablas resultantes de UCINET fueron analizadas y un reporte con la interpretación de esos resultados fue creado para cada clase en la muestra. Los programas de software UCINET, Pajek y MAGE fueron usados para visualizar las interacciones del grupo. Los reportes de ARS para cada caso en el estudio y las visualizaciones creadas fueron presentados a un experto en el área de ARS e interacciones en ambientes virtuales para chequear la precisión del análisis realizado.

Resultados y Discusión

En esta sección, se presentan y analizan los resultados para uno de los cursos de forma detallada. Los resultados del segundo caso se incluyen de manera simplificada. Se discuten y comparan resultados para ambos casos en las conclusiones.

Caso 1

Este curso es uno de los últimos que los alumnos realizan previo a su graduación. En las clases, las interacciones se realizan principalmente por medio del entorno Moodle y emisión de audio en vivo.

La interacción asíncrona fue desarrollada a través de los foros en Moodle. En este curso, el espacio asíncrono tuvo foros abiertos donde todos los estudiantes de la clase podían participar, y otros foros exclusivos para grupos.

La mayoría de las discusiones estuvieron organizadas de modo que cada semana se iniciaba un nuevo tema, pero los estudiantes podían continuar las discusiones iniciadas en semanas previas. Las métricas ARS se calcularon para diferentes matrices de adyacencia: los foros abiertos, los foros exclusivos de los grupos, y todo junto. El número total de mensajes en los foros fue de 1270, de los cuales 976 fueron enviados a los foros abiertos y 294 en los foros grupales. Hubo 26 participantes, incluyendo el instructor y un ayudante de cátedra. Dos de los 24 estudiantes fueron de una promoción anterior.

En la Tabla 1 se muestra la matriz de adyacencia para las interacciones en el espacio en línea. Esa matriz es el resultado de aplicar el programa Perl a los datos ingresados para la interacción de la clase. Los números deben leerse del siguiente modo: el número en la fila i y columna j representa el número de respuestas que el participante en esa fila le envió al participante en esa columna. Por ejemplo, puede verse que A3 envió 6 mensajes a A1, mientras que A1 envió 2 mensajes a A3. Se eliminaron los ceros para mejorar la lectura de la matriz.

	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10	A11	A12	A13	A14	A15	A16	A17	A18	A19	A20	A21	A22	A23	A24	A25
A0		1
A1	2		2	2	1	1	2						1		1	1	6	1	3		1	1	1	1
A2		3	2	1	3		1	1	1	1	1	1	1		4			1		2		1
A3	1	6	1	3	2		3		2	1	4	2	1	3	4		3		2	2	2	2	3	3
A4		2	7	5	24	1	5	2	5	4	2	3	4	9	5	6	3		2	2	5	17	2	2	1
A5		1	1		4	1	2	1			6	3	1	1	1	2	1				3		3	2
A6	2	8	3	4	10	2	10	2	1	3	1	5	3	2	8	3	5	2	2	5	2	4	1	1		1
A7				1			1	1			1	1			2		1				1	1
A8	1			1	3		1	2	1	1	1	3	2	1	6	2	5	5	2	1	5	2	1	2
A9	1	2		1	3	1	3	1	3	1	4	1	3		8	3	2	1		4	4			3	1
A10		3	1		2	4			1	1		1		1	1	2			1		5			1	1
A11		4	1			5	4	1	2	2	3		2	1	2	2	2	2	3	1	2	1	1
A12		4	1	1	3	1	1			2	1	2				1	2		2		2	3	1	1
A13		4	1	2	18	1	5					3	1	3	6	2		2	1	3	1	7		1
A14		5		2	4	2	4			3	2	4	1	4	1	4	2	4	3	3	1			1	2
A15		1	1		10		1	2	1		1		2	1	2	1				3	2	8	1	2	2
A16		7	1	5	2	3	3		1	5		1	2		4	2	3		1	1	3	1		1
A17				3			1		1				2				1		2	1	1			1
A18	1	2	1		2	3			1	1	1	1				2	2	1
A19			2				1				1				4		2			21	1
A20		2		1	1	6					2	1	1			1	2		2		1	1
A21			2		9	1								1	1	2	1		2	1	1	10		1
A22		2		2	1	1			1			1	2	1		2	1				2
A23		3		3	2				2		3		1	1	2	2	2	2		1	2	1		4
A24		1								1		1				1	1	2	1
A25							1												1

Tabla 1. Matriz de Adjacencia (Todos los Foros).

	A0	A1	A16	A3	A23	A5	A10	A11	A20	A22	A4	A13	A15	A21	A2	A6	A14	A7	A19	A17	A8	A9	A24	A12	A18
A0		1
A1	1		3	1
A16		3	2	1
A3		2		3	2
A23		1	1		4
A5						1	2	2	3	2
A10						4		1	3
A11						1	1			1
A20						4	2		1
A22						1			1
A4											22	5	3	14
A13											12	3	1	5
A15											8	1	1	6
A21											8	1	2	10
A2															1	1	4		2
A6															2	9	2	1	5
A14																3	1		1
A7																	1	1
A19															1	1	4		21
A17																					1				1
A8																				3	1				1
A9																					1		1
A24																				2
A12																									1
A18		1				2					1				1						1

Nota. Cada bloque gris delimita un grupo.

Tabla 2. Matriz de Adjacencia (Grupos Solamente), display alternativo.

En la Tabla 2 se muestra la matriz de adyacencia con la interacción de los grupos. Para hacer más evidentes los grupos, se acomodaron los actores en otro orden. Cada bloque grisado delimita un grupo. El instructor (A18) y un estudiante (A12) están al final de la matriz, porque ellos tienen un patrón de interacción diferente.

Si bien este es un estudio en el cual la relación es direccional y valorada, para el cálculo de la densidad, se utilizó la matriz de adyacencia dicotomizada, para que de este modo la densidad represente el porcentaje de la clase que ha interactuado entre sí. Cuando la densidad se calcula con la matriz dicotomizada (cualquier valor mayor a 0 se fija en 1), el valor de la densidad es de .55 con una desviación estándar de .5 (55% de todas las conexiones posibles se efectuaron). Esto puede considerarse un índice de densidad alto para una clase de 26 participantes. Significa que más de la mitad de todos los enlaces posibles se han realizado. La desviación estándar es una medida de la variación entre los elementos. En este caso, la desviación estándar es casi tan grande como la media, implicando que hay una gran variación en los enlaces. Los participantes enviaron entre 1 y 118 mensajes con un promedio de 35 mensajes cada uno (SD: 26).

En esta clase, se formaron 5 grupos de trabajo al principio del semestre. Esos grupos debían completar una tarea y disponían de un foro privado donde unicamente los miembros del grupo podían enviar mensajes. Los grupos se formaron del siguiente modo:

Grupo 1: A8, A9, A12, A17, y A24

Grupo 2: A2, A6, A7, A14, y A19

Grupo 3: A0, A1, A3, A16, y A23

Grupo 4: A4, A13, A15, y A21

Grupo 5: A5, A10, A11, A20, y A22.

Se realizó un análisis de cliques con la matriz de adyacencia que contenía los datos de las interacciones de los grupos, con el fin de ver si el software de redes sociales era capaz de detectar esos grupos formales. Cuando se aplicó la definición de 2-cliques, UCINET detectó 5 formaciones (ver Tabla 3).

El diagrama de árbol (Ilustración 2) muestra la existencia de 5 “entidades”. No obstante, ellas no son exactamente los 5 grupos de la clase. Puede verse que básicamente hay dos niveles, los cuales muestran si los miembros se reúnen (y cuando) o si no lo hacen. Algunos miembros (por ejemplo A12, A9, y A24) nunca se unen, esto es porque tienen participación marginal (o nula) en las discusiones grupales. Observando la Tabla 3, puede verse que con la definición de 2-clique, UCINET pudo identificar perfectamente a los Grupos 4 y 5. Los Grupos 2 y 3 se encontraron con un miembro faltante. El Grupo 1 fue detectado sólo parcialmente y además mezclado con el instructor (A18). Esto no es sorprendente, ya que la interacción del Grupo 1 fue la menos intensa de todos los grupos.

Tabla 3. 2-Cliques.

En la Tabla 4 se muestran resultados de centralidad aportados por las métricas ARS. En verde, los puntajes dentro del 25% más alto, en amarillo el rango intermedio (próximo a los valores promedio), en rojo los valores dentro del 25 % más bajo. En negrilla, el valor promedio, y en azul, se destacó al instructor (A18)

Se incluyen copias de pantallas de las visualizaciones con propósitos ilustrativos, pero para apreciar de manera completa el poder y la belleza de esas imágenes interactivas, las mismas deben ser vistas en una pantalla de computadora (ver Anexo I).

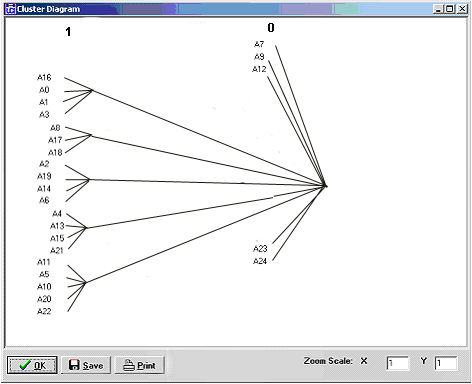
Ilustración 2. Diagrama de árbol para los 2-cliques de los foros grupales.
Se han realizado algunas modificaciones estéticas a la salida gráfica de UCINET para que sea más sencillo de interpretar.

Para crear las visualizaciones se utilizaron algoritmos de resortes embebidos. El uso de algoritmos de resortes embebidos para visualizar datos se basa en la idea de pensar en los puntos como anillos conectados con resortes. El algoritmo busca una solución óptima donde exista una cantidad mínima de fuerza en los resortes que conectan el conjunto completo de puntos (Freeman, 2000). Pajek, el software para ARS, utiliza dos algoritmos: Kamada-Kawai (KK) y Fruchterman-Reingold (FR). El algoritmo FR (Fruchterman & Reingold, 1991) produjo los gráficos más claros, y por esto fue elegido en lugar del KK (Kamada & Kawai, 1989).

Tabla 4. Métricas ARS.

En la Ilustración 3, que fue hecha con Pajek usando el algoritmo FR, puede verse que A25 es un “outsider”; este miembro tiene solo dos conexiones al grupo. A0, A7, A19, A21, A22, A24, y A25 son también marginales.

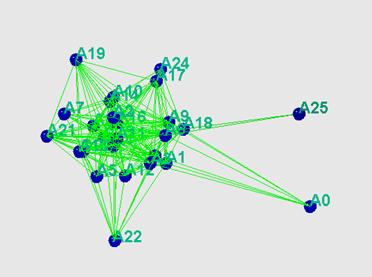
Ilustración 3. Representación MAGE de la clase con información de todos los foros.

En la Ilustración 4, A25 (el soporte técnico de la clase) se ha excluído de los cálculos de las coordenadas. El instructor (A18) y dos aislados (A0 y A24) se han coloreado de un modo diferente para hacerlos mas visibles. Puede verse que esos dos aislados están débilmente conectados y sólo por medio del instructor. A17, A19, A21, y A22 están también en la periferia [de la discusión].

La Ilustración 5 muestra la red cuando se ha aplicado una dicotomización haciendo que los valores mayores a 2 se transformen en 1s en la matriz de adyacencia. Se puede ver ahora una estructura más simplificada (notar que hay varios miembros que ya no están más en la red, ellos han sido borrados porque sus contribuciones fueron mínimas). Puede verse aquí que el instructor (A18) y otros miembros que están en el centro de la red (A1, A3, A4, A6, A9, A11, y A14) han sido coloreados para que se destaquen. Aquí podemos apreciar una configuración “cebolla”: los miembros se sitúan en una configuración de tipo capas, donde la capa más externa está conformada por aquellos miembros más aislados de las conversaciones. Notar también que esta estructura de red no tiene un participante “estrella” central, más bien en su lugar hay algunos “conectores” (como A3, A9, y A13) que vinculan varios miembros en la red.

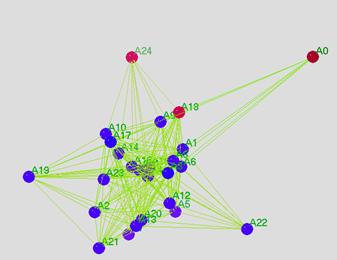
Ilustración 4. Detalle de la actividad del instructor (A18).

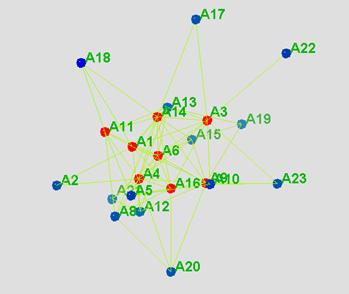
Ilustración 5. Representación dicotomizada de la red de la clase.

La Ilustración 6 muestra una simplificación más profunda. En esta ilustración la red se ha dicotomizado para valores mayores a 4. La imagen muestra más claramente el subgrupo de miembros con la interacción más intensa en la clase. A4, A6, A8, y A14 son los miembros con la mayor interacción y vínculos, ellos están al centro de la red y están interconectados directamente entre todos ellos, excepto por el enlace A6-A8. Notar que el instructor (A18) ya no es parte de la red a este nivel de interacción.

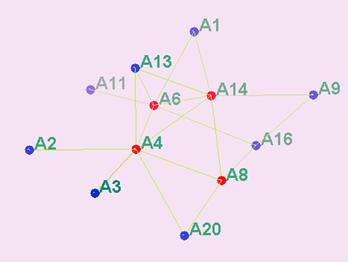
Ilustración 6. Los miembros más interactivos de la clase.

Las imágenes presentadas previamente fueron creadas usando datos de los foros abiertos, el gráfico que se muestra a continuación se creó con datos del foro de grupos únicamente. Cuando se utilizó el algoritmo FR para calcular las coordenadas, una representación sorprendentemente precisa emergió. La dinámica de los grupos se muestra claramente en la Ilustración 7. Puede verse que el instructor (A18) es el único con acceso a todos los grupos, y que un estudiante (A12) no participó para nada en su grupo. El gráfico muestra los 5 subgrupos con sus miembros y las interacciones en cada uno. Puede verse, por ejemplo, que A0 está solo conectado a un miembro de su grupo (Grupo 3), y que en el Grupo 4, todos los miembros están conectados entre ellos. El Grupo 1 está conectado al instructor a través de dos miembros: A8 y A17.

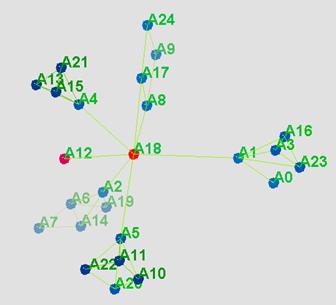
Ilustración 7. Visualización de la actividad de los foros grupales.

Resumen de Resultados ARS para el Caso 1

El análisis conducido lleva a concluir que esta clase ha tenido un alto nivel de interacción y reciprocidad. Esto está confirmado por la densidad de los enlaces, y por las estadísticas de las conversaciones, las cuales mostraron que el 30% de las respuestas fueron a nivel 3 o más alto (nivel 3: al menos 4 mensajes intercambiados). Los participantes contribuyeron a los foros con un promedio de 35 mensajes (SD: 26).

Los participantes más activos fueron: A3, A4, A6, A9, y A14. A4 y A16 fueron los miembros más prolíficos (“fuentes”), mientras A1, A4, A14, A16, y A20 fueron los más respondidos (“sumideros”). A4 fue prolífico y muy respondido, y puede considerarse un “comunicador/facilitador” o “transmisor” de información. A1 fue el participante mas respondido no obstante su contribución a la discusión fue menor al promedio. Ocho participantes: A0, A7, A10, A17, A21, A22, A24, y A25 estuvieron aislados (tuvieron un rol periférico/pasivo en las discusiones). El comportamiento pasivo de A25 se explica porque fue el ayudante de cátedra asignado a la tarea de soporte técnico de la clase. El instructor tuvo una participación “tranquila” en los foros.

Los índices de centralización (grado, intermediación y cercanía) mostraron que en esta clase el poder estuvo bastante distribuído. Las discusiones de la clase no parecen haber sido monopolizadas. El instructor (A18) actuó como un “broker”, conectando los miembros menos poderosos, y no tuvo un rol destacado en las discusiones. La inspección visual de las ilustraciones hechas con MAGE confirmó muchos de los resultados de ARS, como el rol del instructor, la presencia de aislados, y la existencia de algunos “facilitadores”. Esas imágenes también permitieron ver la configuración “cebolla” de la clase, con algunos estudiantes actuando en las capas más internas como puentes (conectores) y otros en las capas más externas, más separados de la discusión. En general, la forma de las interacciones imitó más a una configuración de “todos-conectados” que a una configuración centralizada. La interacción de los grupos fue claramente descrita por los gráficos MAGE, y detectaron la falta de participación de un estudiante (A12).

Caso 2

El análisis del segundo caso del estudio se realizará de manera resumida, dando las características del curso y los resultados obtenidos de modo simplificado, ya que el detalle del caso anterior ilustra los procedimientos empleados. Este segundo curso está a mitad de camino de completarse el programa de maestría. Una pieza importante del curso es un proyecto de aplicación práctica en el que  los alumnos comienzan a trabajar temprano en el curso. En esta clase los ambientes de interacción principales fueron Moodle y Tapped-Inn (un ambiente en línea para interacciones síncronas y asíncronas). La interacción asíncrona se desarrolló a través de los foros de Moodle.

Las discusiones en los foros se organizaron en dos temas semanales. El número total de mensajes en los foros de esta clase fue 1037. Hubo 443 conversaciones y 153 mensajes (inicio de una conversación) sin ninguna respuesta. Hubo 30 participantes; incluyendo dos instructores (un ayudante de cátedra (AC) y un profesor) y un estudiante graduado trabajando como soporte técnico. Veinte estudiantes fueron de la misma promoción, un estudiante de una promoción previa, y seis estudiantes fueron estudiantes del campus de programas diferentes a la maestría en línea.

Resumen de Resultados ARS para el Caso 2

El análisis que se llevó a cabo permite concluir que las interacciones asíncronas en este curso estuvieron centralizadas alrededor del ayudante de cátedra. El puntaje para la densidad fue promedio para una clase de este tamaño, con mucha variación (el número de contribuciones al foro varió de 0 a 133 con una media de 19 y desviación estándar de 24). Los participantes más activos del foro fueron A2 (AC), A3, A6, A8, y A13. A2 (AC) fue el miembro más “influyente” (el que envió más respuestas) y A6 el más “prestigioso” (el que recibió más respuestas). Hubo al menos un tercio de los miembros de la clase que actuaron como aislados, teniendo poca y periférica participación en las discusiones. Los participantes con bajos índices (en todas las medidas) fueron: A1, A9, A11, A17, A20, A21, A23, A24, A25, A26, y A28. Entre esos estuvieron el soporte técnico de la clase y un estudiante que abandonó tempranamente el curso.

Los índices de centralización (grado y cercanía) mostraron una cantidad sustancial de poder en unos pocos miembros de la clase. Los participantes más poderosos (i.e., aquellos con altos puntajes en todas las medidas) fueron A2 (AC), A3, A6, A8, y A13. El comportamiento del profesor (A0) fue muy “silencioso” en los foros, con una participación significativamente menor que su AC.

El software de análisis de redes no logró detectar participantes trabajando en grupos en los foros de este curso. No obstante, por medio de las visualizaciones, los estudiantes que no pertenecen al programa de master han sido señalados como una posible entidad marginal.

La distribución de los mensajes de acuerdo a los niveles de respuestas confirma lo que los gráficos MAGE dicotomizados mostraron: no hay mucha interacción mas allá del nivel 2 (al menos 3 mensajes intercambiados). Este nivel de interacción es característico de un estilo de comunicación de P&R (preguntas y respuestas).

La inspección visual de las figures tri-dimensionales hechas con MAGE permiten afirmar que el ayudante de cátedra estuvo en el centro de las discusiones (ver Ilustración 8), actuando como una “fuente”. La configuración de la red es muy centralizada y muy parecida a la configuración teórica de estrella cuando se la simplifica por medio del proceso de dicotomización.

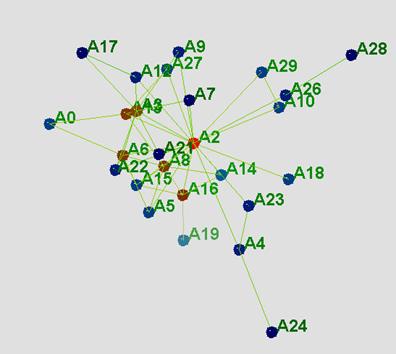
Ilustración 8. Visualización 3D de la interacción de la clase, notar el rol central de A2.

Validación

Se hicieron entrevistas y un cuestionario para los docentes a cargo de los cursos en la muestra, para validar los resultados del análisis con técnicas ARS. Se completaron 3 cuestionarios: 1 en el Caso 1 y 2 en el Caso 2. Los instructores colaboraron y mostraron interés en la investigación. Los cuestionarios se completaron inmediatamente después de concluído el semestre en el cual se desarrolló el curso, a fin de evitar errores por olvido. Antes de completar el cuestionario, los instructores fueron consultados acerca de su experiencia con la enseñanza en línea y en particular con la utilización de foros asíncronos. En todos los casos, los instructores habían tenido experiencias previas de utilización de estas tecnologías en otros cursos.

Se compilaron los resultados de los cuestionarios y se preparó un reporte para cada instructor con un resumen de los resultados de las métricas ARS y la comparación con las respuestas de los instructores al cuestionario. Este fue el material utilizado para las entrevistas que se realizaron luego con los instructores. El reporte incluyó además un enlace a las visualizaciones interactivas creadas con los datos de la clase junto con instrucciones para manipular y jugar con esos objetos. Las preguntas de la entrevista fueron destinadas a recolectar información acerca de la utilidad de las métricas ARS y las visualizaciones, así como también para obtener feedback acerca de la presentación de las imágenes interactivas. Las entrevistas constituyeron otro elemento de validación para el reporte ARS y las visualizaciones.

Los tres instructores que participaron en el estudio fueron muy positivos respecto de los resultados de la investigación y particularmente entusiastas respecto de las visualizaciones. Describieron esas imágenes y las posibilidades que el software provee para manipularlas con entusiasmo. La característica más útil que los instructores vislumbran tendrían las métricas ARS y las visualizaciones es la posibilidad de monitorear la actividad de la clase mientras la misma se desarrolla, y utilizar esas herramientas como sensores para señalar cuando alguien se está quedando atrás o no está comprometiéndose en las conversaciones del curso.     

Conclusión

Los avances en las tecnologías de comunicación e información han favorecido la generación de ambientes de aprendizaje diferentes del salón de clase tradicional, por lo tanto es natural pensar que métodos diferentes de los usados en las aulas convencionales pueden ser los adecuados para investigar lo que ocurre en las mismas. Este estudio examinó la validéz de las técnicas de ARS y visualizaciones como una posible aproximación metodológica alternativa y apropiada.

Este estudio mostró que las métricas ARS y las visualizaciones de interacciones son herramientas útiles y potencialmente efectivas para analizar patrones de interacción en espacios asíncronos en línea. Las métricas ARS y las visualizaciones pueden ayudar a hacer juicios acerca del diseño de la clase, desempeño de la clase, y actuación de los estudiantes. Ellos mejoran la “visibilidad” del curso. Los instructores pueden monitorear las actividades de los estudiantes e identificar potenciales problemas.

Las métricas usadas en este estudio proporcionaron información útil acerca de los patrones de interacción. Algunas de las medidas funcionaron mejor que otras. La medida de densidad probó ser un buen estimador para el nivel de profundidad de las discusiones en los foros, ya que un índice moderado en la densidad estuvo relacionado a un estilo de foro de preguntas y respuestas mientras que un índice de densidad alto estuvo asociado a un foro de discusión más comprometido.

Las medidas de grado (ambas: de salida y entrada), fueron índices muy reveladores. Detectaron a los participantes más activos e influyentes en los foros. También apuntaron a los estudiantes menos activos, con actividad periférica en las discusiones. El índice de intermediación también funciono como un buen indicador de quienes fueron aquellos miembros que actuaron como puentes o conectores entre los participantes de la clase.

La comparación de los resultados del cuestionario administrado a los instructores con los resultados ARS mostró que el uso de las métricas ARS y las visualizaciones pueden revelar información que el instructor desconoce. Algunas discrepancias entre las percepciones de los instructores y los resultados ARS pueden atribuírse al hecho de que las percepciones del instructor están formadas no solo con las interacciones en el foro, sino también con el conjunto completo de actividades desarrolladas en la clase, lo cual incluyó interacciones síncronas y otras comunicaciones asíncronas.

Las visualizaciones interactivas creadas con MAGE hicieron “gráficamente evidente” las medidas ARS obtenidas a partir de los datos de los foros. Esto ayudó a que los participantes de la red descubran sus propios comportamientos. Esos gráficos asisten a los instructores a monitorear las actividades de la clase, revelar participantes marginales, y descubrir participantes dominantes o conectores.

Se espera que los resultados de este estudio provoquen la discusión de nuevas preguntas y asuntos relacionados a interacciones en ambientes en línea, como por ejemplo: ¿Es bueno o no tener una clase con “estrellas”?    ¿Qué aspecto tiene un “buen” patrón de interacción? Si la clase fue exitosa (de acuerdo al instructor y estudiantes): ¿Cómo fue su “forma” o índices ARS?

Bibliografía

Anderson, T., Rourke, L., Garrison, D. R., & Archer, W. (2001). Assessing teaching presence in a computer conferencing context. Journal of Asynchronous Learning Networks, 5 (2).

Aviv, R., Erlich, Z., Ravid, G., & Geva, A. (2003). Network analysis of knowledge construction in asynchronous learning networks, Journal of Asynchronous learning Networks, 7 (3).

Babelas, A. (1950). Communication patterns in task-oriented groups. Journal of the Acoustical Society of America, 22, 271-282.

Barnes, J. A. (1954). Class and committees in a Norwegian island parish. Human Relations, 7, 39-58.

Batagelj, V., & Mrvar, A. (2003). Pajek - Analysis and Visualization of Large Networks. In Jünger, M., Mutzel, P., (Eds.) Graph Drawing Software (pp. 77-103). Berlin: Springer.

Borgatti, S. P., & Everett, M. G. (1992). The notion of position in social network analysis. In P. Marsden (Ed.), Sociological Methodology (pp. 1-35). London: Basil Blackwell.

Borgatti, S. P., Everett, M. G., & Freeman, L. C. (1992). UCINET IV Network Analysis Software. Connections, 15, 12-15.

Boudourides, M. A., Mavrikakis, M., and Vasileiadou, E. (2002). Email threads, genres & networks in a project mailing list, Association of Internet Researchers International Conference, Maastricht, The Netherlands.

Freeman, L. C. (2000). Visualizing Social Networks, Journal of Social Structure 1, 1. http://www.cmu.edu/joss/content/articles/volume1/Freeman.html.

Fruchterman, T., & Reingold, E. (1991). Graph Drawing by Force-Directed Replacement. Software--Practice and Experience 21, 1129-1164.

Galaskiewicz, J., & Wasserman, S. (1994). Introduction: Advances in the social and behavioral sciences from social network analysis. En S. Wasserman & J. Galaskiewicz (Eds.), Advances in social network analysis: Research in the social and behavioral sciences (pp. xi-xvii). Thousand Oaks, CA: Sage.

Hanneman, R. & Riddle, M. (2005). Intruduction to social network methods. Consultado en http://www.faculty.ucr.edu/~hanneman/

Harary, F., & Norman, R. Z. (1953). Graph Theory as a Mathematical Model in Social Science. Ann Arbor: University of Michigan Press.

Inglis, A., Ling, P., & Joosten, V. (2002). Delivering digitally. Managing the transition to the knowledge media (2nd ed.). London: Kogan Page.

Johnson, J. C., Palinkas, L.A., & Boster, J. S. (2003). Informal Social Roles and the Evolution and Stability of Social Networks. En R. Breiger, K. Carley, & P. Pattison (Eds.), Dynamic Social Network Modeling and Analysis (pp. 121-132).Washington, DC: The National Academies Press.

Kamada, T., & Kawai, S. (1989). An Algorithm for Drawing General Undirected Graphs. Information Processing Letters 31, 7-15.

Krackhardt, D. (1987). Cognitive social structures. Social Networks, 9, 109-134.

Moreno, J. L. (1934). Who shall survive?: Foundations of Sociometry, Group Psychotherepy, and Sociodrama. Washington DC: Nervous and mental Disease Publishing Co.

Oliver, M., & Shaw, G. P. (2003). Asynchronous discussion in support of medical education. Journal of Asynchronous Learning Networks, 7(1), 56-67.

Paredes, A. (2007). Santiago de Chile y Mendoza, Argentina: La red social que apoyó a exiliados chilenos (1973-1976). REDES- Revista hispana para el análisis de redes sociales, 13 (4),http://revista-redes.rediris.es

Park, H. W. (2003). Hyperlink network analysis: a new method for the study of social structure on the Web. Connections, 25(1), 49-61.

Richardson, D. C., & Richardson, J. S. (1992). The Kinemage: A Tool for Scientific Communication. Protein Science 1, 3-9.

Scott, J. (2000). Social Network Analysis: A Handbook. Second edition. London: Sage Publications.

Souto-Maior Fontes, B. A., & Eichner, K. (2004). A formação do capital social em uma comunidade de baixa renda. REDES- Revista hispana para el análisis de redes sociales, 7 (2), http://revista-redes.rediris.es

Teves, L., Crivos, M., Martínez, M. R., & Sáenz, C. (2002). Una Aplicación de la Metodología de Redes Sociales a la Investigación Etnográfica, 2 (6),  http://revista-redes.rediris.es

Wasserman, S., & Faust, K. (1994). Social network analysis: Methods and applications. New York: Cambridge University Press.

White, H. C. (1963). An Anatomy of Kinship. Englewood Cliffs, NJ: Prentice Hall.

Anexo I

Puede experimentar con las visualizaciones en esta URL (requiere plugin de Java):

http://online2.exactas.unlpam.edu.ar/willging/sna/images.htm