Reconstruyendo la red de lazos personales. Metodología egocéntrica para investigación sociocéntrica

Pablo De Grande - Universidad Católica Argentina / CONICET[1]

Manuel Eguía - Universidad de Quilmes / CONICET

Resumen

Este artículo presenta los avances de investigación en un modelo computacional que permite describir una red social observada por medio de encuestas muestrales representativas de sus nodos. El modelo tiene también el objetivo de servir a estimar la fiabilidad de la encuesta así como estimar medidas globales de la red.

De esta forma, el trabajo propone un camino alternativo al análisis egocéntrico de datos representativos de redes personales,  obteniendo con un modelo de multiagente de simulación un análisis sociocéntrico de la información parcial de una red.

La medición que se utiliza como marco de referencia empírico del modelo es la producida por la Encuesta de la Deuda Social Argentina en el año 2006. Esta encuesta se aplica anualmente en 1500 hogares del país sobre una muestra polietápica representativa de adultos en Gran Buenos Aires, Córdoba, Mendoza, Neuquén, Salta, Resistencia y Bahía Blanca.

Palabras clave: redes personales, redes sociocéntricas, modelos multiagente, muestreo.

Abstract

This article introduces the preliminary results of a computational network model research approach. The aim of this model is to help estimating sampling errors of an ongoing personal network survey, as well as to describe the network observed.

In this way, it presents an alternative path to the egocentric analysis of representative data of personal networks, using a simulation multiagent model in order to make a sociocentric analysis on partial information of a network.

The survey used as empirical reference frame for the model is the Encuesta de la Deuda Social Argentina (2006), which is applied annually to 1500 household along the country, using a multistage representative sample of adults in 7 large Argentinean cities (Gran Buenos Aires, Córdoba, Mendoza, Neuquén, Salta, Resistencia and Bahía Blanca).

Key words: personal networks, sociocentric networks, multiagent models, sampling.

Introducción

El propósito de este trabajo es presentar los avances de investigación en el desarrollo de un modelo computacional que permita describir adecuadamente una red social observada por medio de encuestas muestrales representativas de sus nodos.

Con frecuencia, las investigaciones sobre redes personales –bajo estrategias egocéntricas de recolección y análisis de la información– se producen desde una perspectiva de observación atomizada del entramado de relaciones sociales: si bien se observan relaciones, se analizan como atributos del nodo conocido (el ego), construyéndose desde los nodos un análisis por agregación mecánica de la red (medias de valores individuales) (Van der Poel, 1993; Wellman y Potter, 1999; Grosetti, 2005; Agneessens et al. 2006).

Esta perspectiva presenta la limitación de tener que prescindir de observaciones generales de la red, devolviendo lo relacional a un nivel de análisis donde los individuos analizados operan metodológica y ontológicamente en independencia unos de otros. Esta operación es particularmente problemática en estudios que, a partir del análisis de redes personales, buscan romper con los supuestos atomistas que hacen de la interacción de los actores un fenómeno irrelevante.

Una red o muchas redes

La preocupación que da origen a este texto es, como se dijo, aquella sobre si la percepción de que existen ontológicamente muchas redes personales, donde cada persona tiene su propia red, no estaría anclada en una perspectiva atomista, desde la cual incluso un análisis relacional puede ser afrontado desde un punto de vista en el que los individuos operan aisladamente unos de otros. Esta preocupación nos llevó a retomar un camino poco transitado en redes personales, que es aquel de abordar el análisis la red como una totalidad (y no como la mera suma de sus nodos).

En este sentido, la cuestión de si se estudian ‘las redes personales’ de los habitantes de una ciudad, o ‘la red’ de vínculos de la ciudad merece particular atención. Con cierto matiz de contradicción, el supuesto existente detrás de afirmar que dos personas tienen dos ‘redes personales’ (una cada uno), pudiéndose en consecuencia comparar a ambas personas tomando a dichas redes como atributos, como posesiones individuales de las que estas personas disponen, relega buena parte de los frutos del análisis de redes tradicional.

Desde esta mirada, el aumento o disminución de la cantidad de vínculos por parte de un individuo es visto en forma independiente del aumento o disminución en la cantidad de vínculos de otra. Sin embargo, estando ambas en un mismo espacio (analítico) relacional, esto es inconsistente.

Por una parte, llevaría a un análisis de una cantidad de redes igual al número de personas, sin que sin embargo se pueda obtener la información de la red ‘completa’ de cada una de ellas (bajo el supuesto poco probable de que en algún punto la lista de conocidos de los conocidos de cada persona encontrara un cierre; esta imposibilidad de clausura de la lista de conocidos de conocidos no hace más que poner en evidencia el carácter inconsistente del enfoque).

Por otra parte, incluso si se tomara una posición de compromiso y se evaluara la red de cada individuo como una red independiente, a partir de información limitada a una cantidad parcial de ‘contactos’, se caería a su vez en problemas estadísticos en cuanto al conteo de los fenómenos, debido a que dos redes atribuidas a diferentes personas pueden constituir parcialmente el mismo dominio empírico (el mismo grupo de vínculos y personas), lo que provocaría un fenómeno de sobreregistración de fenómenos que ocurren en los nodos más conectados (las redes individuales más grandes tendrían más probabilidades de ser muestreadas en repetidas ocasiones que las redes más pequeñas).

Una posible solución a estos problemas radica en retomar la mirada de la red como una red única, donde el objeto a explicar es un objeto macrosociológico, a saber, la red de lazos interpersonales como entidad analítica que abarca y ordena la mirada de la totalidad de lazos interpersonales existentes en un cierto espacio y tiempo (y no como una tasa o un valor construido para una población como un agregado de datos individuales, tal como la tasa de desempleo o el producto bruto interno nacional).

Bajo este esquema, cabe estudiar ‘las redes’ (en plural) o bien allí donde no pudiera existir una conexión entre dos grupos de nodos, o bien por un propósito comparativo que conduzca a delimitar el campo de vínculos a analizar en grupos diferenciados relacionalmente entre sí (construyendo así por ejemplo un estudio entre las redes personales dos comunidades rurales dada una cierta coyuntura).

Esta operación de observación de la red como espacio social permite interpretar las encuestas sobre ‘redes personales’ no en el sentido de ‘las redes personales de los encuestados’, sino como descriptas del los modos de inserción de cada persona individual en la red completa de vínculos personales. La red, asimismo, puede presentarse fragmentada en grupos de vínculos aislados entre sí (llamados ‘componentes’ en la terminología de ARS), sin dejar estos por ello de ser parte de la red en tanto pueden reconectarse, así como desconectarse los ahora conectados, en resumen, mientras pueden todos seguir una dinámica común dentro del espacio de nodos y conexiones analizado.

En esta perspectiva, la información obtenida constituye evidencia muestral de puntos de una red total, de la cual es posible construir estimadores que la describan y caractericen. Asimismo, conocidas las características de esta red total, es posible también evaluar las probabilidades para diferentes grupos de personas de situarse en nodos con características específicas. De esta manera, si por ejemplo la red posee un 8% de nodos conectados a personas con estudios universitarios, es posible evaluar las probabilidades condicionadas de ocupar dichos lugares a partir de atributos individuales (externos a la red, tales como edad, sexo, capital cultural, etc.) o propios de la red (como al cantidad de vínculos, el nivel de intercambios o la persistencia de estos para el nodo en cuestión). De esta forma, puede explorarse en qué medida es más probable que alguien con bajo capital cultural ocupe un lugar vinculado a personas universitarias, así como cuánto una mayor cantidad de vínculos aumenta tales probabilidades.

En este contexto, la observación de las redes en una población (por nombrar algunas: la red de asociaciones profesionales, la red de activistas sindicales, la red personal de adultos, la red de la infancia, la red de los adolescentes, entre tantas otras) constituye un nuevo observable, sin por decir esto suponerlo aislado o ajeno a debates y problemas de más larga tradición en ciencia social.

El contexto empírico

Como se mencionó anteriormente, este modelo fue producido a la par de un relevamiento sobre vínculos personales. Este relevamiento fue un módulo complementario de la Encuesta de la Deuda Social en su edición de 2006, que se realiza en 1500 hogares de 7 grandes centros urbanos de Argentina[2] (ODSA, 2007).

El módulo presentó un generador de nombres que refería a vínculos de apoyo, permitiendo nombrar hasta cinco personas[3]. El propósito de este ítem fue relevar una muestra de vínculos fuertes en diferentes espacios sociales, cubriendo en forma homogénea distintos rangos de edad, niveles socioeconómicos y sexos entre la población adulta[4].

En la encuesta se relevaron alrededor de 1500 vínculos, que se repartieron entre la mitad de la muestra, mientras que la otra mitad declaró no tener vínculos para nombrar. Sobre estos vínculos, se relevó información de edad, sexo, nivel educativo, tipo de vínculo, frecuencia de contacto, antigüedad, origen del vínculo y grado de conocimiento entre los vínculos. Este trabajo la información que se utiliza remite a la cantidad de vínculos y la transitividad o densidad producto del nivel de conocimiento entre los vínculos de cada entrevistado.

Muestreo de grandes redes

En sus inicios, el análisis de redes sociales se ha basado en el relevamiento de la totalidad o la gran mayoría de los vínculos que conformaban las redes estudiadas. Esto ha posibilitado el desarrollo de herramientas de inferencia estadística, análisis estructural y modelización de redes de muy diversa índole (Wasserman, 1994).

Sin embargo, poco a poco la necesidad de estudiar redes sociales más amplias se ha puesto de manifiesto. Una de las limitaciones para llevar esto a cabo manteniendo la modalidad de observar la red completa es la tasa a la que crece la cantidad de posibles conexiones en una población: para un pequeño pueblo de 5 mil personas, la cantidad de nodos posibles asciende a 12 millones (Granovetter, 1976). Por este motivo –aunque también por la economía de toda investigación hecha sobre poblaciones numerosas– se ha avanzado en algunas estrategias, recomendaciones y técnicas referidas al problema del muestreo de redes, que abarca tanto el problema de contactar a un número reducido de nodos, como al de tomar un grupo parcial de los vínculos presentes en cada uno de ellos[5].

En primer lugar, cabe mencionar dos grupos de problemas que inciden en la elaboración de una muestra, ambos de alcance general a muestras no reticulares. El primero remite a la posibilidad de que una persona responda adecuadamente un cuestionario sobre vínculos, siendo estos extensos y capturando información no necesariamente clara para el encuestado (como lo son otras preguntas demográficas, como tener o no calefacción, su nivel educativo, etc.) (Erickson 1981). El segundo grupo remite a cuestiones de la identificación y localización de los miembros de la muestra, individualizando la disponibilidad o no de la lista completa de la población para construir la muestra, el carácter o no aleatorio de esa construcción y el carácter aleatorio o no de las no-respuesta (Erickson, 1986). En nuestro espacio de investigación empírica, estos problemas son abordados por estrategias habituales en encuestas de hogares, y su detalle excede el alcance de este artículo.

En segundo lugar, existen dificultades para tomar muestras en redes que se derivan de su naturaleza reticular. Estas son la no-independencia estadística de los atributos de sus nodos y la existencia de distribuciones no normales de ciertas medidas reticulares (Ove, 1978; Ove, 2005). Como consecuencia, en redes sociales complejas, muchas de las hipótesis de independencia estadística y normalidad (en la distribución de sus magnitudes) que subyacen a las teorías estándar de muestreo pueden resultan inaplicables.

Asimismo, cabe considerar que es esperable que redes con mayor o menor concentración de vínculos, o con estructuras en mayor o menor grado aleatorias, presenten diferencias a la hora de elaborar muestras debido tanto a la existencia de nodos o regiones aisladas entre sí como a las distribuciones esperables de vínculos en función de la transitividad de cada red.

En este artículo, se propone evaluar la utilidad de un modelo de simulación como marco de trabajo en el cual experimentar empíricamente con algunos de los problemas de representatividad de muestro en redes con alta transitividad y bajo número de vínculos.

Simulación de redes sociales

La simulación computacional de redes sociales forma parte del campo más amplio de la simulación como técnica de creación de teoría y validación empírica en ciencia social. El incremento en la capacidad de procesamiento, unido a la mayor flexibilidad conceptual que aportaron los modelos multiagente como técnica de modelado (Macy y Willer, 2002), provocaron en las últimas dos décadas la difusión de iniciativas de simulación en una diversidad de áreas (Gilbert y Troitzsch, 1999). La introducción de estos abordajes supone nuevos desafíos en la formalización de modelos en ciencia social, complejizando y extendiendo la posibilidad de análisis y organización de sus resultados de investigación (Axelrod, 1997).

Mayoritariamente por medio de modelos multiagente, se han desarrollado modelos de simulación de redes, que permiten observar y variar las condiciones de dichas redes experimentando sobre los factores que influyen en caracteres y mecanismos de sus dinámicas.

El modelo que se presenta en este artículo tiene su anclaje en una investigación sobre redes personales, y se vincula por ello con modelos que problematizan los mecanismos de creación de vínculos por búsqueda local (Vázquez 2003, Marsili et al 2004) y de distancia social (Wong et al. 2006).

Otras áreas temáticas características de los modelos de simulación de redes sociales son la adopción de innovaciones (Gilbert et al., 2001); epidemiología (Eubank 2005);  organización del tráfico urbano (Rossetti y Liu 2005); resiliencia de organizaciones terroristas (Moon y Carley, 2007) y la formación de opinión y consenso (Stocker et al 2001).

El modelo

El modelo propuesto está basado en un esquema generativo de vínculos que preserva las características estructurales observadas en un gran número de redes sociales: alta transitividad, un grado considerable de homofilia y una gran variabilidad en la cantidad media de vínculos por individuo.

La red generada por el modelo consta de un número fijo de agentes (o nodos) que establece nuevos vínculos mediante dos mecanismos diferenciados: a)  a través de los vínculos ya existentes y b) a partir de cruces fortuitos con otros agentes. El caso (a) es referido en la literatura de redes como ‘búsqueda local’ y corresponde a la situación en la cual los agentes tienen la posibilidad de ampliar su red de vínculos de forma transitiva: se vinculan con los contactos de sus contactos. Este proceso de crecimiento de los enlaces tiende rápidamente a formar cliqués dentro de las redes y es esencial para poder reflejar la alta transitividad observada en las redes sociales. Sin embargo, es insuficiente en sí mismo para hacer crecer los vínculos a partir de una red dispersa. El mecanismo (b) resume a toda otra circunstancia que potencialmente podría generar nuevos vínculos y a diferencia del anterior si posibilita el crecimiento global de la red de enlaces, ya que bajo este mecanismo todos los agentes se ven entre sí y son susceptibles de establecer un vínculo.

Por otra parte, los enlaces tienen una volatilidad inherente, que aspira a reflejar por un lado el decaimiento natural de los lazos interpersonales y por otro la rotación y variabilidad observada en los vínculos en muchas redes sociales. Esta volatilidad se implementa en el modelo mediante un mecanismo de borrado aleatorio de los vínculos, de tal forma que cada enlace posee una vida media determinada (con una variabilidad estadística que sigue una ley exponencial). Sin embargo, debido al mecanismo de búsqueda local y la implementación de la distancia social que se detalla más adelante, existen también vínculos ‘altamente probables’ que se restablecen luego del borrado.

El modelo incorpora también un esquema simplificado de distancia social, mediante la cual la probabilidad de establecimiento de vínculos entre los nodos varía. Los enlaces potenciales generados por los mecanismos detallados anteriormente son efectivizados sobre la base del cómputo de la distancia social del potencial vínculo. Dicha distancia social incorpora únicamente aquellas variables susceptibles de registro que podrían tener incidencia a la hora de decidir si el lazo entre dos agentes es más o menos probable.

En el presente trabajo el foco fue puesto sobre dos atributos en particular: la localización geográfica y el nivel educativo. Cada individuo está dotado de estos dos valores para estos atributos, que se mantienen fijos a los largo de la simulación. La distancia social entre dos individuos participantes de un vínculo determinado, se computa como una media pesada de la distancia geográfica y la diferencia entre sus niveles educativos. El vínculo se consolida con una probabilidad que es inversamente proporcional a dicha distancia.

Más específicamente, el modelo propuesto evoluciona con un paso temporal discreto Dt, y en cada paso de  iteración se actualiza el estado del sistema recorriendo secuencialmente a cada agente. Para cada uno de ellos se realiza la siguiente serie de acciones:

1)      Búsqueda local. Con probabilidad P₁*Dt, el agente a se pone en contacto con un conocido de un conocido. Este nuevo contacto b es establecido de forma permanente con una probabilidad P­₂ que depende de la distancia social los agentes a y b:

            

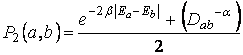
Donde E_a y E_b son los niveles educativos de los agentes a y b, y D_ab la distancia geográfica entre ambos agentes (calculada mediante la métrica Manhattan, es decir, la distancia en calles o cuadras desde una localización a la otra).

Los parámetros α y β controlan la tasa de decrecimiento de P­₂ (la probabilidad de establecer el vínculo) en función del aumento de las distancias geográfica y educativa respectivamente.

De esta forma, valores altos de β corresponden a un marcado decrecimiento de P­₂ cuando aumenta la diferencia de niveles educativos entre los agentes evaluados (promoviendo una fuerte homofilia). A medida que decrece este parámetro, la probabilidad de establecer vínculos con agentes con niveles educativos diferentes aumenta. De forma análoga, valores pequeños de α corresponden a mayor probabilidad de vincularse con agentes alejados geográficamente.

2)      Búsqueda global. Con probabilidad P­₃*Dt el agente a es puesto en contacto con otro agente c extraído al azar de la población. Al igual que en el paso anterior, este vínculo se consolida con una probabilidad P₂ que depende de la distancia social entre los agentes a y c.

3)      Volatilidad. Con probabilidad P­₄*Dt, el agente a pierde uno de sus vínculos.

Parámetros de ejecución

En las simulaciones para redes con transitividad, los valores de parámetros fueron establecidos en P­₁=0,25, P₃=0,01 y P₄=0,03. Los parámetros α y β, que controlan P­₂, fueron establecidos en 1,0.

Las redes simuladas son observadas luego de 11 mil ciclos, utilizando Dt=0,01, período en el que sus medidas globales muestran valores estacionarios.

Para la construcción de la redes aleatorias, se utilizaron como parámetros P1=0,00, P3=0,05 y P4=0,03, manteniendo los demás factores constantes.

La condición inicial para las simulaciones de redes con transitividad es una red aleatoria donde existen tantos vínculos como agentes, para permitir el desenvolvimiento inicial de las búsquedas por conocidos.

Resultados

Distribuciones muestrales

Para caracterizar el problema muestral se generaron dos tipos de redes: (a) una red aleatoria sin transitividad basada en el modelo descripto en la sección anterior pero sin búsqueda local y (b) una red generada con el modelo y con características estructurales compatibles con las medidas de la Encuesta de la Deuda Social Argentina (en cantidad media de vínculos y transitividad).

El objetivo de estas simulaciones fue mostrar el grado de fiabilidad de los valores inferidos de diferentes magnitudes estructurales de las redes a partir de muestras de diversos tamaños.

Para ello se simuló una realización de gran tamaño (100 mil individuos) de cada uno de los subtipos de red evaluados. A continuación se extrajeron M muestras aleatorias de N individuos. Para cada muestra se calcularon los valores medios sobre la población de N individuos de su cantidad de vínculos.

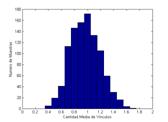
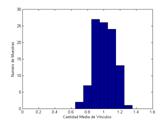
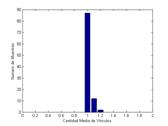
Los resultados obtenidos para cada una de las redes se muestran en las figura 1 para tres tamaños de la muestra (N=10, N=100 y N=1000). En todos los casos se ilustra el valor medio sobre el espacio de M muestras (M=100).

Tipo de red/ tamaño          muestral	n=10	n=100	n=1000
Aleatoria	Figura 1.a	Figura 1.b	Figura 1.c
Con vínculos por búsqueda local (transitividad)	Figura 2. a	Figura 2 b.	Figura 2.c.

 Figura 1. Distribución de las muestras en redes aleatoria y con transitividad.

Fuente: Elaboración propia basada en salidas del modelo.

Los dos sets de muestras del modelo reflejan un fenómeno esperado, que es el cambio en la forma de la distribución. Este cambio en la distribución hace particularmente crítico el problema del muestreo en las redes con transitividad, pues al volverse asimétrica su distribución la moda (el valor más esperable) y la media no coinciden.

Asimismo, la dispersión de las muestras decrece a medida que aumenta la cantidad de casos, siendo la dispersión en ambas redes similar (con un rango entre 0,85 y 1,15 en la red aleatoria y entre 0,95 y 1,25 en la red con alta transitividad).

A este respecto, si bien no es posible extrapolar mecánicamente las distribuciones del modelo a la red observada, los resultados permiten no descartar la hipótesis de que en una cantidad cercana a 1000 casos, para una red dispersa (k~1) con alta transitividad (0.6), es posible suponer niveles de confianza similares a aquellos que se derivan de una estimación estadística (a partir de la varianza en las observaciones).

Al interior de la red

El segundo uso que se planteó para el modelo es poder reproducir cualitativamente características de algunas condiciones parciales de la red. En este sentido, es posible observar en las encuestas de campo parámetros correspondientes a diferentes grupos, espacios y categorías sociales. En la figura 4 pueden verse los niveles medios de cantidad de vínculos y transitividad (densidad) observados según el nivel socioeconómico de la zona donde se tomó el caso.

		Cantidad de vínculos	Transitividad (densidad)
Nivel socioeconómico del barrio	Muy Bajo	.79	.68
	Bajo	.77	.59
	Medio Bajo	1.03	.66
	Medio/medio	1.11	.58
	Medio Alto	1.20	.63

 Figura. 4. Cantidad de vínculos y transitividad (densidad) promedio observados según nivel socioeconómico del barrio (radio censal).

Fuente: Elaboración propia en basada en información de la Encuesta de la Deuda Social Argentina (2006)

A partir de estas observaciones, se produjeron dos redes que se ajustaran a los parámetros observados (densidad constante, cercana a 0,6, y k variando entre 0,8 y 1,20), de tamaño N=1000, que permitieran reconstruir redes similares en valores medios a aquellas de barrios de nivel Medio Alto y Muy Bajo.

Sin que el análisis detallado de estas redes forme parte del presente artículo, en las figuras 5 y 6 se presenta las salidas de estas redes ‘zonales’.

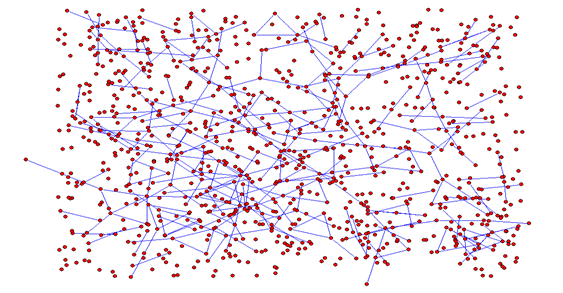
Figura 5. Red generada por el modelo ajustando a valores K=0.7, densidad=0.6 (Zona 1, NSE Muy Bajo)

 

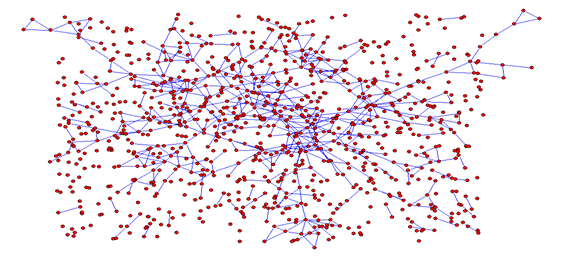
Figura 6. Red generada por el modelo ajustando a valores K=1.2, densidad=0.6 (Zona 2, NSE Medio Alto)

El contraste entre ambas figuras permite observar dos fenómenos de interés.

En primer lugar, la densidad alta y sostenida junto al aumento de vínculos, produce en la Zona 2 la mayor presencia de nodos con niveles más elevados de vínculos, como centros de grupos relativamente cerrados y numerosos. Este tipo de grupos es más infrecuente en la Zona 1, viéndose grupos con nodos más desvinculados (no tan densos en su interior) y distribuidos en casi todo el espacio.

Esta combinación permite suponer que en redes con las características de la Zona 2 los fenómenos de centralidad pueden ser más relevantes que en la zona con menor número de vínculos. El bajo número de vínculos promedio, no impide por sí mismo el fenómeno de una red más jerárquica, donde los vínculos se produzcan con nodos que centralicen las interacciones. Sin embargo, no se observó este un mecanismo ni bajo las reglas del modelo, donde los nodos conectados lo hacen en forma horizontal, ni en los casos observados, donde no se detectaron casos atípicos con cantidades muy elevadas de vínculos.

En segundo lugar, la alta cantidad de nodos desconectados en la red correspondiente a la Zona 2 (a pesar del aumento en la cantidad total de vínculos) puede ser vista como la contracara de la alta transitividad. Un aumento en la cantidad media de nodos de la Zona 2 respecto a la Zona 1 pudo haber provocado en una baja en la cantidad de nodos desconectados. Sin embargo, se hace notar en el diagrama cómo esto no se produce, lo que mostraría cómo la alta transitividad (el efecto del crecimiento de los vínculos por medio de conocidos de conocidos, o la práctica de que los vínculos cercanos terminen conociéndose) logra absorber este aumento de los vínculos sin que redunde en una cantidad mayor de personas conectadas.

Conclusiones

La necesidad de reinsertar el análisis macro, o ‘sociocéntrico’, en los estudios de redes personales fue el punto de partida para este trabajo.

En este sentido, se mostró la factibilidad de ajustar un modelo generativo a las principales medidas estructurales observadas en un relevamiento típico de redes personales (basado en un generador de nombres y un relevamiento muestral de la red). Estos parámetros conocidos no fueron introducidos en forma directa valores fijos en los nodos (o agentes), sino que operaron como variables de resultado del modelo.

La utilidad del trabajo se estableció en dos dimensiones: la estimación de la confianza muestral, y la observación ‘panorámica’ de la red.

En el primer aspecto, la varianza de las medias muestrales para un tamaño de muestra mayor (mil casos) mostró una importante reducción respecto a muestras menores, si bien en la red con transitividad la singularidad de su distribución asimétrica se mantuvo en todos los tamaños muestrales, con su consecuente impacto en la fiabilidad de los estimadores.

Referido al segundo punto, queda abierto un campo de observación, tanto desde la mirada de la red total como desde miradas parciales de situaciones específicas. En la sección anterior se mostraron escenarios correspondientes a parámetros obtenidos en diferentes espacios sociales concretos (barrios con niveles socioeconómicos Medio altos y Muy bajos), poniendo de relieve fenómenos poco visibles en las medidas iniciales (tales que la ‘desigualdad distributiva’ en el aumento de los vínculos), así como nuevos interrogantes que reformulan posteriores intervenciones.

Como en todo trabajo de investigación, la obtención de sus resultados van ligados al precio de aceptar supuestos y limitaciones de los modelos teóricos y metodológicos que se adoptan. Los modelos multiagente no son la excepción, padeciendo restricciones de escala y confiabilidad estadística en sus resultados. Al mismo tiempo, su principal virtud es quizás la flexibilidad en la elección de reglas y funcionamientos no-lineales que es posible incorporar en ellos, pudiéndose especificar aspectos contextuales y de interacción local típicamente ignorados en otros tipos de modelos.

Sin duda es esta flexibilidad, unida a la ausencia de modelos estadísticos con los cuales resolver la totalidad de cuestiones vinculadas a la representación de redes observadas, la que permite hacer de estos modelos un complemento valioso en el análisis de redes sociales extensas. En este artículo se presentaron algunas evidencias en este sentido, las que cabrá continuar como parte de la investigación en curso.

Bibliografía

Agneessens F., Waegea H. y Lievensa J. (2006). “Diversity in social support by role relations: A typology”, Social Networks, 28(4), 427-441.

Axelrod, R. (1997). “Advancing the Art of Simulation in the Social Sciences”. En Conte, R.; Hegselmann, R. y  Terna, P. (eds.): Simulationg Social Phenomena, 21-40, Berlin, Springer.

Burt R. (1984). “Network items and general social survey.” Social Networks 6(4), 293-339.

Erickson B. y Nosanchuk, T. (1983). “Applied network sampling”, Social Networks (5) 367-382.

Erickson B., Nosanchuk, T. y Lee E. (1981). “Network sampling in practice: some seconds steps”, Social Networks (3) 127-136.

Eubank S. (2005). “Network Based Models of Infectious Disease Spread”, Japanese Journal of Infectious Diseases, Vol. 58, 6, S9-S13.

Gilbert N., Pyka A. y Ahrweiler P. (2001). “Innovation Networks - A Simulation Approach”, Journal of Artificial Societies and Social Simulation, vol. 4, no. 3.

Gilbert, G. N. y Troitzsch, K. G. (1999). Simulation for the Social Scientist, Open Univ. Press.

Granovetter M. (1976). “Network Sampling: Some First Steps”, The American Journal of Sociology, Vol. 81, No. 6 (May, 1976), pp. 1287-1303.

Grossetti M. (2005). “Where do social relations come from? A study of personal. networks in the Toulouse area of France”. Social Networks (27), 289-300.

Macy, M. W. y Willer, R. (2002). “From factors to actors: Computational Sociology and Agent-Based Modeling”. En Annual Review of Sociology, n° 28, 143-166.

Marsili M., Vega-Redondo F., Slanina F. y Wachter F. (2004). “The Rise and Fall of a Networked Society: A Formal Model”, Proceedings of the National Academy of Sciences of the United States of America, 101, No. 6, 1439-1442.

Mc Carty C., Bernard H., Killworth P., Shelley G. y Johnsen E. (1997). “Eliciting representative samples of personal networks”, Social Networks (19) 303-323.

Moon I. y Carley K. (2007). “Modeling and Simulating Terrorist Networks in Social and Geospatial Dimensions”, IEEE Intelligent Systems, Vol. 22, No. 5, 40-49.

ODSA (2006). Cuestionario de la Encuesta de la Deuda Social Argentina. Recuperado el 15 de 12 de 2006, de Observatorio de la Deuda Social: http://www.uca.edu.ar/esp/sec-investigacion/esp/subs-observatorio/page.php?subsec=cuestionarios

          - (2007). “Apéndice I: Análisis metodológico aplicado a la Encuesta de la Deuda Social Argentina”. En Barómetro de la Deuda Social Argentina. Buenos Aires: Educa.

Ove F. (1978). “Sampling and Estimation in Large Social Networks”, Social Networks, 1, 91-101.

          - (2005). “Network sampling and model fitting”, en Carrington P., Scott J. y Wasserman S. (comps) Models and Methods in Social Network Analysis, New York: Cambridge Univ. Press, 31-55.

Rossetti, R. y Liu, R. (2007). “A dynamic network simulation model based on multi-agent systems”. En Klügl F., Bazzan A. y Ossowski S. (eds.) Applications of Agent Technology in Traffic and Transportation, 181-192. Berlin, Birkhäuser.

Sawyer, K. (2003). “Artificial Societies - Multiagent Systems and the Micro-Macro Link in Sociological Theory”. En Sociological Methods & Research, vol. 31, n° 3, Londres, SAGE publications, 325-363.

Stocker R., Green D. y Newth D. (2001). “Consensus and cohesion in simulated social networks”, Journal of Artificial Societies and Social Simulation, vol. 4, no. 4.

Van der Poel, M. (1993). “Delineating personal support networks”. Social Networks, 15(1), 49-70.

Vázquez A. (2003). “Growing network with local rules: Preferential attachment, clustering hierarchy and degree correlations”, Physical Review E, 67, 056104, 1-15.

Wasserman S. y Faust K. (1994). Social Network Analysis, Methods and Applications (Structural Analysis in the Social Sciences). New York: Cambridge Univ. Press.

Wellman B. y Potter S. (1999). "The elements of personal commuties", en Networks in the Global Village, Westview Press, 49-81.

Wong L., Pattison P. y Robins G. (2006). “A spatial model for social networks”, Physica A, 360, pp99–120.