Vol.3,#3, sept-nov. 2002.
http://revista-redes.rediris.es
Macro-micro-macro
y modelos estadísticos para redes
[1]
ICS, University
of Groningen (Holanda)
Abstract
For empirical work on
macro-micro-macro issues, it is indispensable to have statistical models
reflecting in a plausible way the data structures and theoretical relations
that are the basis of such issues. A basic family of models for macro-micro
effects is provided by multilevel analysis. An important way of studying
micro-macro transitions is by means of simulation.
Network modeling provides another, particularly
appropriate, approach to macro-micro-macro issues. Network models represent, in
a more subtle way than multilevel models, that what can be observed at the
macro level is the result of phenomena at the micro level, while these
phenomena themselves are conditioned by the macro level. The use of appropriate
statistical network models, with sufficient attention to model fit, can lead to
important progress in our understanding of macro-micro-macro issues. This is
more a matter of promises for the future than of past achievements, however. A
major reason for the limitations in the current state of the art is that the
feedback issues which are essential to how networks operate, are so difficult
to express in statistical models in a manageable and plausible way.
In models for single (i.e., one-moment) observations of a
social network, the time dimension of the feedback process is beaten flat,
which leads to grave difficulties both of interpretation and of mathematical
modeling. Although modeling single observations of social networks still is
necessary and useful, more insight may be gained from repeated (multi-moment)
observations of social networks. If such a dynamic model would include not only
the relations between actors but also changing actor attributes (e.g.,
attitudes, behavior, performance) and the larger pattern of social settings in
which networks are embedded, it would capture a great part of what we regard as
macro-micro-macro processes. Such an integrated model does not yet exist, but
work is currently under way toward the construction of this type of models.
Resumen
Para llevar a cabo el trabajo empírico sobre temas macro-micro-macro, es indispensable tener modelos estadísticos que reflejen de manera plausible la estructura de los datos y las relaciones teóricas en la base de tales cuestiones. Una familia básica de modelos para los efectos macro-micro es ofrecida por el análisis multinivel. Una manera importante de estudiar las transiciones micro-macro es mediante simulación.
Los modelos sobre redes proponen
otra perspectiva, particularmente apropiada, a los temas macro-micro-macro. Los
modelos de redes representan, de manera más sutil que los modelos multinivel,
que lo que puede ser observado a nivel macro es el resultado de fenómenos a
nivel micro, mientras que estos fenómenos están condicionados por el nivel
macro. El uso de modelos estadísticos apropiados para redes, con atención
suficiente al ajuste del modelo, puede conducir a progresos importantes en
nuestra comprensión de las cuestiones macro-micro-macro. Sin embargo, esto es
más una promesa de cara al futuro que un logro del pasado. Una razón de
importancia mayor de las limitaciones en el estado actual del arte es que las
cuestiones de retroalimentación (feedback) que son esenciales en cómo operan
las redes, son extremadamente difíciles de expresar en modelos estadísticos de
forma operativa y plausible.
En los modelos para una única
observación (en un momento dado) de una red social, la dimensión temporal de la
retroalimentación es aplastada, lo que conduce a dificultades graves tanto de
cara a la interpretación como al modelado matemático. A pesar de que modelar
observaciones en un momento dado de las redes sociales es todavía necesario y
útil, es posible ganar en comprensión a partir de observaciones repetidas de
redes sociales (en varios momentos diferentes). Si tal modelo dinámico
incluyese, no sólo las relaciones entre actores, pero también los atributos
cambiantes de los actores (por ejemplo, las actitudes, comportamientos,
resultados) y las pautas englobantes de los contextos sociales en que las redes
se encuentran inmersas, capturaría una gran parte de lo que consideramos como
procesos macro-micro-macro. Tal modelo integrado no existe todavía, pero se
están llevando a cabo avances hacia la construcción de este tipo de modelo.
Introducción
Las cuestiones sobre la relación entre
macro-micro-macro (MMM) tratan sobre la explicación de fenómenos al
nivel macro, basándose en teorías sobre el comportamiento de los actores al
nivel menor, comprendidos en el nivel macro del sistema. Tal como lo expresa el
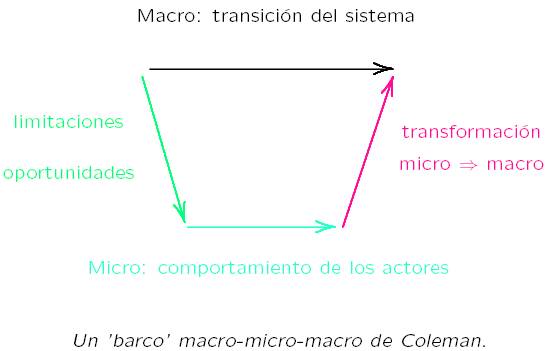
esquema (Figura 1) del “barco” de Coleman (1990), el nivel macro es un sistema
en transición. El nivel macro impone limitaciones y oportunidades a los
actores. Estos, en el nivel micro, desarrollan comportamientos que a su vez
inciden en la transformación del nivel macro.
Figura 1: El ‘barco’ macro-micro-macro de
Coleman
El análisis de redes sociales ofrece un
marco excelente para el análisis de las relaciones macro-micro-macro: el
contexto de la red es, para cada actor, una parte importante de su conjunto de
oportunidades y limitaciones. La atención aquí se centra en situaciones en que
los lazos relacionales entre actores son considerados como parte de su
comportamiento (p.e. selección de relaciones): la red es endógena en el modelo.
En este contexto, consideramos como nivel macro la totalidad de la red
estudiada; como nivel micro la red personal de cada actor. El “barco” de
Coleman aplicado al análisis de redes sociales sería el siguiente:
Figura 2: El ‘barco’ de Coleman aplicado a
las redes sociales
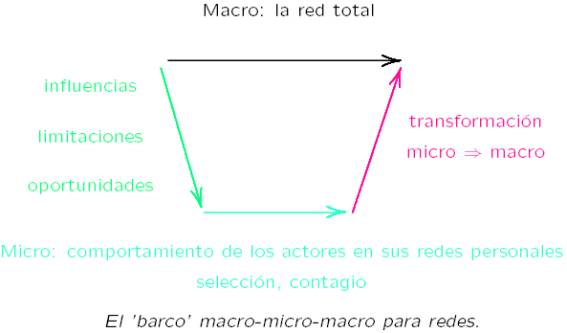
La red total constituye el contexto de
limitaciones, oportunidades e influencia sobre los actores. Al nivel micro, y
teniendo en cuenta el contexto, los comportamientos de los actores inciden en
sus redes personales; estos pueden seleccionar sus relaciones (o su forma, o su
contenido) y ejercer influencia sobre ellas (ya sea de manera voluntaria o
involuntaria). A su vez los comportamientos de los actores afectan de manera
directa o indirecta las redes personales de los otros actores. Finalmente, como
efecto de los comportamientos individuales y las (re)configuraciones de las
redes personales de estos, la estructura de conjunto, la red total, se ve
transformada.
En la modelización estadística de temas
macro-micro-macro, los actores individuales son concretos y los contextos
también son concretos: grupos, organizaciones, redes, etc. Como en cualquier
otro análisis estadístico, la variación de conjunto en la base de datos tiene
que ser comparada con la ‘variación en la dirección predicha’.
Para estudiar la relación macro-micro-macro
en contextos más tradicionales con datos no relacionales, se utiliza el análisis
multinivel o modelo jerárquico lineal (hierarchical linear model)
para más información ver Snijders y Bosker (1999).
Este artículo se centra en cuestiones de
investigación en que las relaciones son la variable dependiente.
A modo de ilustración, consideremos un grupo que produce un bien común para sus
miembros, por ejemplo un grupo deportivo. Consideremos la siguiente hipótesis:
“los grupos multifuncionales muestran más variación en el nivel del bien común
producido que los grupos unifuncionales” es decir, que algunos producen un
nivel muy alto y otros uno muy bajo. El argumento teórico de esta hipótesis
inspirada por Flache (1996) y Lindenberg (1998) consiste en que en los grupos
multifuncionales las relaciones son más múltiples; las sanciones contra los
comportamientos aprovechados en las díadas múltiples tienden a ser positivas
más que negativas; las sanciones positivas son más efectivas que las negativas.
Esto conduce a un nivel de producción mayor del bien común perseguido, a no ser
que el grupo se especialice en la producción de otro bien común, en cuyo
caso el primer bien común es producido a un nivel más bajo. Desarrollemos el
ejemplo del grupo deportivo: en principio el bien común de un grupo deportivo
suele ser la producción de resultados en el deporte practicado (ganar partidos,
obtener mejores marcas...). Si este grupo es multifuncional, es decir que
comparte otras actividades u objetivos, por ejemplo salir los fines de semana o
confiarse sobre cuestiones personales, es más probable que los miembros tiendan
a estimularse de manera positiva, p.e. animándose mutuamente, en sus
actuaciones deportivas. En principio estas sanciones positivas mejorarán los
resultados deportivos del grupo a no ser que el objetivo principal del grupo
deje de ser la producción de resultados deportivos y pase a ser pasarlo bien o
constituir un grupo de amigos, en cuyo caso la producción de resultados
deportivos puede dejar de ser tan importante y probablemente sea menor que la
inicial (pero la producción de diversión mayor).
La relación a nivel micro debe ser
investigada. En nuestro enunciado ejemplo: “en las díadas múltiples las
sanciones tienden a ser positivas” la unidad de análisis es la díada. En un
diseño de investigación, podríamos operacionalizar la medida de las variables
que nos interesan (multiplexidad y sanciones), mediante una pregunta
dirigida a los actores j estructurada, por ejemplo, de la siguiente
manera: “¿Si i percibiera que usted tiene un comportamiento aprovechado,
le sancionaría? Y si lo hiciera ¿de qué manera?”. De este modo, tanto la
variable independiente (multiplexidad) como la variable dependiente (sanciones)
son variables relacionales. Esto desplaza la atención de una cuestión que trata
sobre grupos multifuncionales a una cuestión sobre díadas múltiples, tal vez en
un grupo.
Hay una cuestión complementaria: cuando se
comparan dos díadas en dos grupos diferentes, las dos díadas teniendo la misma
multiplexidad, ¿existe un efecto adicional del grado de multifuncionalidad del
grupo en su conjunto -tal vez operacionalizada como la media de multiplexidad
diádica- sobre las formas de las sanciones en las díadas? Este aspecto
multinivel es dejado fuera de estudio en el presente artículo. Por el
momento, consideremos la red como compuesta por un solo grupo de personas.
Para tratar cuestiones sobre variables
relacionales, cuando hay datos disponibles, el modelo p2 (van Duijn
1995, van Duijn y Lazega 1999, Boer et al. 2002) o p* también
llamado modelo exponencial de grafos aleatorios ERGM (exponential random
graph model) (Frank y Strauss 1986, Wasserman y Pattison 1996) serían en
principio apropiados para el análisis estadístico. La desventaja del modelo p2
es que puede modelar los efectos reticulares de manera limitada: incluye
efectos diádicos pero no puede tratar efectos triádicos. La desventaja del
modelo p*, por otra parte, es que el método de estimación pseudoprobable
(pseudolikelihood estimation) con regresión logística tiene una validez
dudosa; las estimaciones ML (maximum likelihood) basadas en Marco Chain
Monte Carlo (MCMC) no siempre dan buenos resultados (Snijders 2002). El
problema no es técnico o algorítmico, sino que reside en la relación entre la
teoría y el modelo estadístico: el modelo de ERGM no es satisfactorio.
Aunque algunas cuestiones teóricas se pueden expresar más fácilmente en modelos
longitudinales que en modelos transversales, en este caso el problema no es la
naturaleza no longitudinal: se puede hacer una crítica similar al modelo SIENA
(Snijders 2001, Boer et al. 2002.) que es un modelo longitudinal.
Problemas con el modelo micro
Hay por lo menos 4 maneras de considerar el
modelo ERGM / p*.
1.
Como lo
expresa la fórmula:
![]()
Donde Y es el grafo aleatorio del que y es
el resultado; z(y) es un vector de un estadístico relevante de la red
(por ejemplo la densidad, el número de díadas recíprocas, el número de
tripletes transitivos, etc.), y q
es el parámetro estadístico desconocido a priori que indica las
magnitudes de los diferentes efectos contenidos en z(y).
2.
Es,
hasta ahora, el único modelo disponible que permite estudiar la transitividad y
otros efectos reticulares no diádicos z(y).
3.
Puede
ser fundado en postulados de independencia condicional utilizando el teorema de
Hammersley-Clifford (ver Frank and Strauss 1986).
4.
Es la
distribución estacionaria bajo un modelo en que las variables de las relaciones
cambian aleatoriamente con “preferencias” dependiendo de los efectos
reticulares z(y).
El problema respecto al punto 3 es que el modelo p*
está fundado en postulados de independencia condicional, que no son siempre
creíbles o plausibles: por ejemplo, un grafo de Markov: Para diferentes actores
i, j, h, k, las variables arco Yij, Yhk son
independientes.
Figura 3: independencia condicional
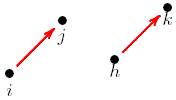
El problema respecto a los puntos 2 y 4 es que las
elecciones habituales por defecto de los efectos reticulares z(y) no son
suficientes. Por ejemplo, para grafos no dirigidos, la primera elección por
defecto suele ser:
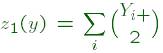
número de estrellas-2,
![]()
número de triángulos.
En la mayoría de los casos hay más estructura
social que la reflejada por estos dos efectos. La estructura no realista expresada utilizando
sólo estos efectos reticulares conduce al comportamiento patológico del modelo
de que un parámetro positivo bastante grande q2 conduce a una
preferencia mayor por grafos con una densidad cercana a 1.0.
Figura 4. Densidad de un digrafo simulado para ERGM con un parámetro
de transitividad moderado.
Densidad
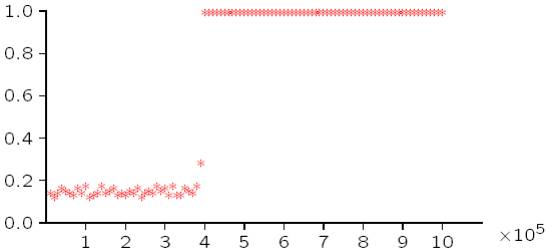
iteración
En el modelo longitudinal SIENA el mismo problema
aparece aunque de modo menos rápido. La operación de SIENA implica que sólo se generan
grafos con la densidad observada (luego no hay problemas de estimación), pero
el modelo SIENA con un efecto positivo de transitividad suficientemente grande
también es atraído hacia el grafo completo (propiedad asintótica del modelo
aleatorio). También para el modelo SIENA, en que los actores tratan
aleatoriamente de optimizar su función objetiva, una función objetiva tal que:
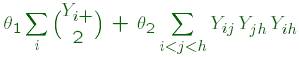
números ponderados de estrellas-2 y triángulos,
no es muy realista. Este modelo micro tiene
consecuencias al nivel macro extrañas y poco atractivas: atracción hacia un
grafo completo, tendiendo a una de densidad de 1, cuando el parámetro de transitividad se vuelve moderadamente
grande. Esto tiene que ver con las dos limitaciones más importantes del modelo
micro:
1.
La
distribución del grado (degree) no es realista- y la distribución del
grado está ligada con la distribución de estadísticos estructurales tales como
el número de tríadas.
2.
Falta la
estructura de oportunidad: para todas las redes, excepto las muy pequeñas, hay
una estructura de oportunidad que debería ser incluida en el modelo.
Hay tres maneras de solucionar estos problemas:
1.
En los
casos en que ERGM / p* es realista, es decir principalmente en las redes
pequeñas, se deben condicionar los grados de entrada y salida en el
análisis estadístico. Esta opción ya está disponible en el modelo SIENA versión
1.96.
2.
Se puede
utilizar un modelo diferente en el que se trate primero el número de relaciones,
y que esté separado del resto de la estructura.
3.
Extender
el modelo con un modelo que tenga en cuenta la estructura de oportunidades.
Una elaboración del punto 2, en concreto mediante
un modelo orientado por el actor (actor oriented model) sugiere
un modelo micro en dos pasos: Para las redes observadas en un momento dado y
las redes longitudinales, en que las distribuciones para las redes observadas
en un momento dado sean consideradas como distribuciones que limitan las redes
dinámicas. Esta opción combina un tratamiento estático y dinámico.
En este modelo los actores i tienen dos
distribuciones de preferencias. Una:
![]()
para el número de relaciones emitidas, y otra para
la estructura de la red:
![]()
Utilidad aleatoria y eliminación mediante atributos.
En momentos aleatorios, los actores pueden cambiar
las relaciones que emiten. Primero deciden si añaden una relación, la
eliminan, o se mantienen constantes, maximizando:
![]()
Una vez tomada la decisión sobre d (añadir, mantener, eliminar una relación), en el caso en que la decisión haya sido que conviene añadir una relación (d=+1), o eliminar una relación (d=-1), sólo entonces deciden sobre qué lazo se efectuará dicha operación maximizando:
![]()
sobre los alters permitidos j. Esto mantiene
el grado (degree) a un nivel razonable para cualquier preferencia
estructural fi2(y), y es intuitivamente plausible.
Este modelo orientado por el actor podría ser
modificado para convertirse en un modelo orientado por larelación o la díada.
El tercer punto sugiere modelar la estructura de
oportunidades: los contextos (settings). Esta opción es la
desarrollada por Pattison y Robins (2002); apoyándose en Verbrugge (1977) ,
Feld (1981) y muchos otros; ver también el trabajo desarrollado actualmente por
Flap y Völker (en Lilnet 2002). Los contextos (settings) son
oportunidades concretas de contacto social: ya sea la localización geográfica,
las organizaciones sociales (escuela, trabajo, asociaciones y clubes...), los
conjuntos de personas ligados informalmente mediante transitividad (notemos que
se trata de una variable endógena), o el producto de conjuntos de actores
dependientes unos de otros. La incorporación adecuada de los contextos en los
modelos de las redes ayuda a hacer los modelos aplicables a una mayor variedad
de tamaños de redes, lo que se llama “modelado multi-escala” (‘multiscale
modeling’). Los contextos exógenos pueden ser modelados mediante
variables explicativas (covariates) de las cuales dependen probablemente
las relaciones, por ejemplo la distancia geográfica, la pertenencia a la misma
organización... Esto es relativamente simple. Los contextos endógenos
pueden ser modelados mediante estructuras parciales de dependencia (partial
dependence structures), tal como lo sugieren Pattison y Robins (2002).
Figura5: Dependencia parcial: dependencia condicional entre Yij y
Yhk si hay una relación j->h, es decir Yjh=1
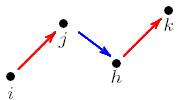
Otra posibilidad es considerar valores múltiples
ordenados para las relaciones. Es decir, primero la distinción entre la
existencia o ausencia absoluta de una relación (por ejemplo un actor conoce la
existencia de otro) y el nivel de intensidad en una escala ordenada de valores
de esa relación (por ejemplo esos actores pueden ser meros conocidos, o amigos,
o mejores amigos).
Los contextos latentes pueden ser modelados
añadiendo un componente al modelo basado en la distancia: existe una estructura
latente de distancia y la probabilidad de una relación disminuye con la
distancia. Diversos autores han sugerido tipos de distancias diferentes: Hoff,
Raftery y Handcock (2002) sugieren la distancia euclídea; Schweinberger (en
Lilnet 2002) propone la distancia ultramétrica; otra posibilidad es tener en
cuenta dos (o más) distancias y considerar en ese caso que la distancia mínima
determina la probabilidad de existencia de una relación (Watts 2002).
Volvamos ahora al aspecto multinivel. Para
comprobar las teorías macro-micro-macro es necesario que haya suficiente
variación en los contextos. Esto puede ser obtenido en una única red de gran
tamaño, lo que se llama ‘modelado multiescala integrado’ (integrated
multiscale modeling) o mediante varios grupos más pequeños, llamado
‘modelado por niveles separados’ (separate level modeling), la elección
depende de lo que sea más conveniente y natural. En cualquier caso, es
apropiado modelar con coeficientes aleatorios, como con el modelado
multinivel. Esto puede ser incorporado directamente en el modelo p2. Un
modelo multinivel simplista ha sido propuesto para SIENA en Snijders y
Baerveldt (2002); está previsto efectuar nuevos desarrollos en el modelo:
coeficientes aleatorios para distinguir los contextos – tres tipos de unidades
de análisis: contextos, actores, relaciones y tal vez un
cuarto actos relacionales.
En conclusión, por el momento disponemos de las siguientes
técnicas útiles:
1.
p* / ERGM con estimaciones Marco Chain
Monte Carlo condicionales en los grados (degrees).
2.
SIENA
para datos longitudinales.
3.
Incluir
los contextos exógenos en los modelos mediante variables.
4.
Modelos
de dependencia parcial.
5.
Modelos
latentes métricos.
Todos ellos pueden beneficiarse de mejoras
ulteriores.
Las técnicas que deberían y podrían desarrollarse
son las siguientes:
1.
Implementaciones
accesibles de las anteriores.
2.
Modelos
de dos pasos de eliminación por aspectos EBA (elimination by aspects) ;
el primero para el grado (degree) y el segundo para la estructura.
3.
Modelos
de redes para categorías relacionales ordenadas (p.e. grado de intimidad de la
relación).
4.
Modelos
multinivel para redes.
5.
Modelos
para dinámica simultánea de redes y comportamientos.
6.
Modelos
para actos relacionales.
Bibliografía
Boer, P., Huisman, M., Snijders, T.A.B., y
Zeggelink, E.P.H. (2002). StOCNET: An open software system for the advanced
statistical analysis of social networks. Version 1.3. Groningen: ProGAMMA/ICS.
http://stat/gamma.rug.nl/stocnet/.
Coleman, J.S. (1990). Foundations of Social
Theory. Cambridge, Massachusetts: Belknap Press of Harvard University Press.
Feld, S. (1981). “The
focused organization of social ties”. American Journal of Sociology, 36,
1015-1035.
Flache, A., M.W. Macy
(1996). “The Weakness of Strong Ties: Collective action failure in a highly
cohesive group”. Journal of Mathematical Sociology 21:3-28.
Flap, H. and Volker, B.
(2002). “Occupational
community and solidarity at work” presentado en la III Conferencia Temática
Europea para Analistas de Redes Sociales, LINET: “La relación Micro-Macro”,
Lille (Francia), Mayo 30-31.
Frank, O., and D. Strauss.
(1986). “Markov graphs”. Journal of the American Statistical Association,
81 (832- 842).
Hoff, P., Raftery, A.,
Handcock, M. (2002). “Latent space approaches to social network analysis”, Journal
of the American Statistical Association, in press.
Lindenberg, S.M. (1998).
“Solidarity: Its Microfoundations and Macrodependance. A Framing Approach.” (61 – 112) en P. Doreian, and T.J.
Fararo (Eds.). The Problem of Solidarity: Theories and Models. Amsterdam:
Gordon and Breach.
Lazega, E., y van Duijn, M.A.J. (1997). “Position in
formal structure, personal characteristics and choices of advisors in a law firm:
a logistic regression model for dyadic network data”, Social Networks,
19 (375-397).
Pattison, P. y Robins, G.
(2002). “Neighborhood-based models for social networks” (301-337) in Sociological
Methodology, editado por R.M. Stolzenberg. Boston and London: Basil
Blackwell.
Schweinberger, M. y
Snijders, T. (2002). “Settings
in social networks: Representation by latent transitive structures” presentado
en la III Conferencia Temática Europea para Analistas de Redes Sociales, LINET:
“La relación Micro-Macro”, Lille (Francia), Mayo 30-31.
Snijders, Tom A.B, (2001).
“The Statistical Evaluation of Social Network Dynamics” (361-395) en Sociological
Methodology, editado por M.E. Sobel and M.P. Becker. Boston and London:
Basil Blackwell.
Snijders, Tom A.B. (2002).
“Markov Chain Monte Carlo Estimation of Exponential Random Graph Models”. Journal
of Social Structure, Vol. 3, No. 2.
Snijders, Tom A.B, and
Baerveldt, Chris (2003, To be published). “A Multilevel Network Study of the
Effects of Delinquent Behavior on Friendship Evolution”, Journal of
Mathematical Sociology.
Snijders, T. A. B. Bosker.
R. (1999). An introduction to basic and advanced multilevel modelling. SAGE.
Van Duijn, M.A.J. (1995). “Estimation of a random
effects model for directed graphs”. In T.A.B. Snijders (Ed.) SSS’95 Symposium
Statistische Software, nr. 7. Toeval zit overal: programmatuur voor random
coëfficiënt modellen (113-131). Groningen: ProGAMMA.
van Duijn y Lazega (1999). Ver Lazega yvan Duijn
(1997).
Verbrugge, L.M. (1977) “The
structure of adult friendships”. Social Forces 56 (576-597).
Watts, D., Dodds, P. y
Newman, M. (2002). “Identity and search in social networks”. Science 296
(1302-1305).
Wasserman, S.y Pattison, P. (1996). “Logit models and logistic regression for social networks: I. An introduction to Markov graphs and p*”. Psychometrika, 61, (401 – 425).