REDES-
Revista hispana para el análisis de redes sociales
Vol.8,#4, Agosto 2005
http://revista-redes.rediris.es
El juego de la red de difusión [1]
Thomas W. Valente [2], Johns Hopkins University (USA)
Es difícil encontrar herramientas de aprendizaje efectivas, entretenidas, realistas y asequibles. Al intentar explicar el análisis de redes y la difusión de la innovación a los estudiantes, se me ocurrió que se podría diseñar una actividad que los estudiantes pudieran hacer en clase para aprender los principios básicos. Por eso diseñé el juego de la red de difusión, fácilmente adaptable, que es instructivo en las lecciones que enseña, y que puede llevarse a cabo de múltiples formas.
El juego requiere de un conjunto de fichas de plástico para el póquer (compré un conjunto de 9 dólares que incluye 100 fichas blancas, 50 rojas y 50 azules, que también utilizo para enseñar los conceptos de muestreo para encuestas) y de una clase o un grupo deseoso de participar. El número óptimo se sitúa entre 20 y 50 estudiantes, pero cualquier tamaño de clase o grupo mayor de 15 podría valer. Presentaré el enfoque básico y los resultados que obtuvimos, y luego presentaré algunas variaciones con las que extender este tipo de ejercicio.Antes de la clase, se utilizó un listado de los estudiantes en clase para crear un cuestionario-lista (apéndice A) pidiéndole a los estudiantes que señalasen los recuadros de aquellos otros estudiantes en la clase con los que (1) pasaron su tiempo libre, (2) comieron juntos en los últimos tres meses, y (3) discutieron sobre temas de salud [3]. Se recogieron los cuestionarios y se utilizaron para crear tres sociogramas y ordenar por rango las puntuaciones de grado de salida (out-degree). Mientras que se analizaban los datos, se impartió una clase de una hora sobre el papel de la comunicación interpersonal y el análisis de redes. Se hizo una pequeña pausa durante la cual se devolvieron los cuestionarios a los participantes.
Se introdujeron dos versiones del juego: (1) las curvas de difusión de la “brecha CAP”, y (2) la influencia de las redes sobre la difusión. La brecha CAP se diseña para demostrar las curvas de difusión que muestran que la conciencia de una innovación (también conocida como conocimiento) precede a una actitud positiva, que precede a la práctica (o adopción). Los académicos han sabido desde hace mucho que la difusión de una innovación sigue un patrón en forma de S como una curva de crecimiento o una función logística (Pemberton, 1936; Rogers, 1995; Valente, 1993; Mahajan & Peterson, 1985). Sin embargo, antes de que se dé la difusión, los individuos deben estar al tanto de que la innovación existe, y luego han de tomar la decisión de probarla. La difusión del conocimiento y la actitud ocurren antes que la práctica/adopción, y esos factores basados en la información pueden difundirse más rápidamente que la práctica. Consecuentemente, hay una demora entre el momento en el que una persona se entera de la existencia de una innovación y el momento en el que la adopta. Esa demora es conocida como “la brecha CAP” (la brecha conocimiento-actitud-práctica), y reducirla es la meta de muchas intervenciones (Chaffee & Roser, 1986; Hornik, 1989).
La brecha CAP es un concepto clave en la teoría del cambio de comportamiento, pero a veces los estudiantes tienen dificultades para comprenderla. Además, la forma de las curvas de difusión (o las funciones de producción) indican la localización de una audiencia en términos del tamaño de la brecha CAP existente, y cómo de rápido (o de lento) está aumentado (o reduciéndose) a lo largo del tiempo. Por eso las curvas de difusión son una herramienta de diagnóstico y evaluación excelentes para la comprensión de la brecha CAP. En consecuencia, hay muchas oportunidades para enseñar curvas de difusión.
Juego 1: La brecha CAP. El primer juego se inició poniendo una transparencia con las siguientes cuatro reglas:
- Sólo puedes darle una ficha a aquellas personas que hayas nominado (las que has elegido en la encuesta). Sólo le pasas fichas a otros al comienzo de un turno. (En otras palabras, no es posible conseguir una ficha durante una “vuelta” y pasarlo inmediatamente a otra persona).
- Para recibir una ficha azul debes tener previamente uno blanco. Para recibir una ficha roja debes tener previamente una azul.
- Sólo puedes pasar una ficha a una persona en cada ocasión, pero puedes darle una ficha a tantas personas como estés conectado. Por ejemplo, si tengo tres fichas blancas, dos azules y una roja, puedo pasar dos blancas a dos personas diferentes con las que estoy conectado, y una azul otra persona con la que estoy conectado.
- Una vez que tienes una ficha de un color quieres mantenerla, pero más de una ficha de un color no es útil para ti, así que por favor pásalo.
Se eligieron tres números aleatorios y se proporcionaron 45 fichas de cada color a las tres personas que correspondían a dichos números (yo tenía 32 estudiantes en clase, de forma que pude usar un dado de 30 caras para seleccionar los números semi-aleatorios).
En este juego las fichas blancas se refieren al conocimiento (conciencia), las fichas azules a las actitudes (decisión), y las fichas rojas a la práctica (adopción). De esa forma, la difusión del conocimiento (blanco) debería ocurrir más rápidamente que la de la actitud (azul), que a su vez debería ocurrir más rápidamente que la práctica (roja). Los tres colores corresponden por tanto a la brecha CAP. Los datos del primer juego se recogen en el Gráfico 1.
Ocurrió que la primera persona elegida al azar tenía la puntuación más alta de grado de salid (out-degree), de forma que la difusión del conocimiento se produjo rápidamente y demostró claramente la brecha CAP. En tiempo cero, el punto de partida, hay una persona que es consciente, una persona en la etapa de la actitud y uno que ha realizado la adopción. Entonces comenzamos el juego permitiendo a los estudiantes que se levantaran de sus sillas y que diesen fichas a aquellas personas con las que estaban conectados, según se indicaba en sus cuestionarios (y que tuviesen las fichas de color requeridas, tales como disponer de una ficha azul antes de recibir una roja). Después de que terminaban de intercambiar las fichas, se les pedía que levantasen la mano para mostrar cuántas personas tenían fichas blancas, azules y rojas. Entonces se puede escribir en la pizarra (o en la transparencia) el número de cada categoría. A continuación se repite el proceso de intercambio de fichas por tres, cuatro, cinco o más veces, hasta que se alcance la saturación o se queda parado.
Gráfico 1. Juego 1, Ensayo 1: Ejercicio de “la brecha CAP”con tres iniciadores al azar.
| Etapa |
Tiempo |
|||||
| 0 |
1 |
2 |
3 |
4 |
5 |
|
| Conocimiento (Blanco) |
1 |
29 |
29 |
31 |
32 |
32 |
| Actitud (Azul) |
1 |
2 |
5 |
8 |
14 |
16 |
| Práctica (Rojo) |
1 |
1 |
1 |
1 |
1 |
2 |
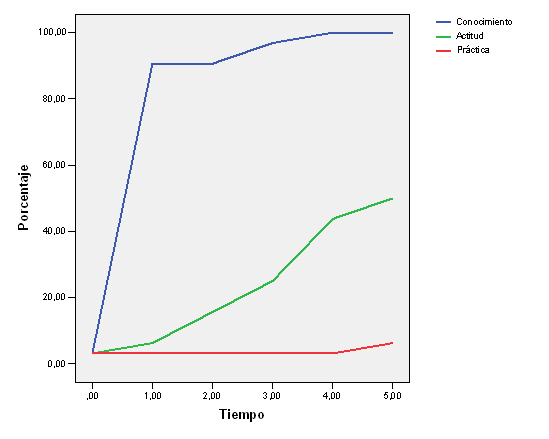
El juego de la red de difusión. Ejercicio de la brecha CAP
En este ejemplo el grupo saturó en conocimiento bastante rápido, mientras que la actitud y la práctica crecieron más lentamente. La saturación de conocimiento ocurrió rápidamente porque la primera persona con conciencia del hecho podía pasar dicha conciencia a mucha otra gente (dándole una ficha blanca a todos aquellos con los que estaba conectado), puesto que tenía muchas nominaciones y no había restricciones en cuanto a quién podía darle las fichas (no hacía falta que ninguno de ellos tuviese una ficha de otro color). Así que la difusión del conocimiento ocurrió rápidamente por dos razones: (1) el comienzo aleatorio para las fichas de conocimiento fue una persona con elevado grado de salida (out-degree), y (2) no había restricciones de personas a quienes dar las fichas de conocimiento. Contábamos con más de un 95% de conocimiento en el primer período de tiempo, y se alcanzó un 50% de actitud en el quinto período de tiempo. Sin embargo, incluso después de cinco períodos de tiempo, la práctica estaba relativamente a un bajo nivel. Para reiterar la lección aprendida, se realizó un segundo ensayo de este juego con tres nuevos inicios al azar. Los datos y las curvas se muestran en el Gráfico 2.
El segundo ensayo también empezó con la distribución de 45 fichas a cada uno de los tres inicios al azar, pero en este caso los tres iniciadores tenían puntuaciones de grado de salida (out-degree) relativamente similares (con un rango de 7 a 9). El segundo ensayo contó con un crecimiento del conocimiento más lento que el primero, puesto que la persona inicial en la difusión de la conciencia contaba con menos nominaciones. El segundo ensayo tuvo un crecimiento en actitud similar al primero, y un más rápido crecimiento en la práctica. Las fluctuaciones en las tasas de crecimiento CAP entre ensayos son una función del número de lazos de salida (out-degree) que poseen los iniciadores al azar, y de los subsecuentes lazos de sus lazos y así sucesivamente. El Gráfico 2 informa de los datos en el segundo ensayo, y muestra cómo el conocimiento, la actitud y la práctica comienzan en el mismo nivel. El conocimiento creció más rápidamente que la actitud y la práctica, puesto que el conocimiento podía trasladarse a todos los contactos de un individuo, y no sólo a aquellos que contasen con la ficha requerida. La brecha CAP se mantuvo en los diferentes períodos y se amplió con el tiempo, pero la brecha entre actitud y práctica era pequeña.
Gráfico 2. Juego 1, Ensayo 2: segundo ejercicio de “la brecha CAP”con tres iniciadores al azar.
| Etapa |
Tiempo |
||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
| Conocimiento (Blanco) |
1 |
7 |
7 |
11 |
17 |
18 |
22 |
| Actitud (Azul) |
1 |
2 |
5 |
8 |
14 |
12 |
14 |
| Práctica (Rojo) |
1 |
1 |
1 |
1 |
1 |
11 |
12 |
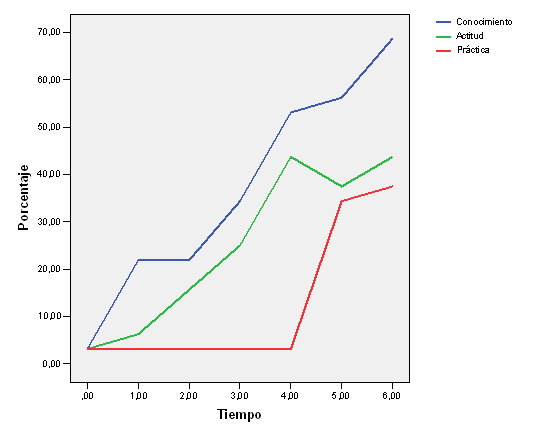
El juego de la red de difusión. La brecha CAP, ejercicio 2.
Si la “brecha CAP” es un concepto importante, aún de mayor interés teórico es la relación entre la estructura de la red y el comportamiento de adopción/difusión. Muchos, si no todos, los programas de cambio planificado se basan en métodos aleatorios o ad hoc para el reclutamiento de nuevos usuarios y definir la población diana de las intervenciones. Este ejercicio está diseñado para mostrar cómo reclutar primero a los líderes de opinión acelera el proceso de difusión. Este juego compara las curvas de difusión cuando los adoptantes iniciales se ajustan a tres condiciones diferentes, correspondientes a la adopción inicial por parte de líderes de opinión, marginales e iniciadores elegidos aleatoriamente.
La segunda versión del juego está diseñada para demostrar cómo la estructura de la red influye en la velocidad de la difusión. El segundo juego representa sólo la adopción-difusión (no el conocimiento, la actitud o la decisión), pero compara la velocidad de difusión dependiendo de si los adoptantes iniciales son miembros centrales en la red o marginales. Si la adopción inicial la realizan líderes de opinión, la difusión ocurre más rápidamente, mientras que si la adopción inicial la realizan marginales ocurre más lentamente.
El modelo básico del líder de opinión plantea que la adopción temprana por parte de líderes de opinión acelera la difusión de una innovación (Valente, 1995). Los intentos de alcanzar una masa crítica de adoptantes se centran por tanto en el reclutamiento de líderes de opinión para aumentar la velocidad del proceso de difusión. Por el contrario, la adopción temprana por parte de marginales (individuos en la periferia) o de aquellos menos centrales produciría curvas de difusión que crecen más lentamente. Este juego proporciona evidencia empírica para apoyar dicha teoría.
Juego 2: Estructura de la red. Para llevar a cabo el segundo juego, propuse un nuevo conjunto de reglas, que eliminaban la número dos de más arriba. Las nuevas reglas son:
- Sólo puedes darle una ficha a aquellas personas que hayas nominado (las que has elegido en la encuesta). Sólo le pasas fichas a otros al comienzo de un turno. (En otras palabras, no es posible conseguir una ficha durante una “vuelta” y pasarlo inmediatamente a otra persona).
- Sólo puedes pasar una ficha a una persona en cada ocasión, pero puedes darle una ficha a tantas personas como estés conectado. Por ejemplo, si tengo tres fichas blancas, dos azules y una roja, puedo pasar dos blancas a dos personas diferentes con las que estoy conectado, y una azul otra persona con la que estoy conectado. Nota: Puedes dar fichas de diferentes colores a la misma persona durante un turno.
- Una vez que tienes una ficha de un color, quieres mantenerlo, pero más de una ficha de un color no es útil para ti, así que pásalo, por favor.
Este juego se construyó para comparar directamente los efectos de comenzar la difusión con (1) líderes de opinión (LO), designados por un alto grado de salida (out-degree); (2) adoptantes seleccionados aleatoriamente (A), o (3) marginales (M), designados por un bajo grado de salida (out-degree) [4]. Repartí 15 fichas rojas a cada uno de los tres LO; 15 blancas a cada uno de los tres A; y 15 azules a cada uno de los tres M. Cualquier diferencia encontrada en la difusión es, entonces, simplemente el resultado de los nodos de partida, puesto que no estamos modificando la estructura de la red de ningún otro modo.
Los resultados se recogen en el Gráfico 3. La difusión ocurrió más rápidamente en la condición de líderes, en comparación con la condición aleatoria, que a su vez fue más rápida que la condición marginal. Después de una aplicación del segundo juego, dibujé las curvas de difusión y expliqué a la clase el propósito del ejercicio, y cómo demostraba las condiciones de difusión. Entonces mostré los sociogramas [5] que generaron un considerable interés en la clase.
Gráfico 3. Juego 2, Ensayo 1: ejercicio de la red de difusión con tres iniciadores para cada condición.
| Condición |
Tiempo |
|||
| 0 |
1 |
2 |
3 |
|
| Líderes (Blanco) |
3 |
20 |
24 |
26 |
| Aleatorios (Azul) |
3 |
11 |
12 |
15 |
| Marginales (Rojo) |
3 |
4 |
4 |
5 |
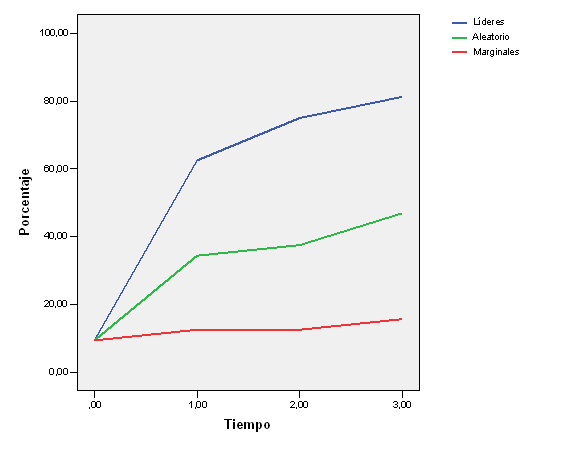
El juego de la red de difusión. La brecha CAP, ejercicio 2.
Estos ejercicios fueron ilustrativos para los estudiantes (y para nosotros) y nos aportaron una serie de lecciones aprendidas y posibles extensiones que otros quizás deseen conocer para hacer uso de esta actividad. Informamos de cinco lecciones y cinco extensiones:
- Con frecuencia fue más fácil preguntar por la incidencia que por la prevalencia en cada nuevo período de tiempo. Es decir, podría simplemente preguntar: “¿Cuántos blancos nuevos?” o “¿Cuántos rojos nuevos?”. Y añadir dicho número al total. Esto también ayudaba a enseñar la diferencia entre incidencia y prevalencia (y saturación)[6].
- Subrayé repetidamente la importancia de los marginales que hacen de puente en la difusión, para evitar así la estigmatización de aquellos que tenían pocas nominaciones.
- Los participantes son extremadamente sensibles sobre la formulación de las preguntas, y dedican mucho espacio a contarte cómo interpretaron las preguntas. Una sugerencia fue pedir a la gente que dijera con quién pasaba el tiempo libre fuera de la Universidad.
- En un ensayo tuvo dos marginales que tenían al menos un lazo, pero que resultó que estaban conectados entre sí. Comprueba que tus marginales no están sólo conectados entre sí.
- Hubo un problema al no tener a todos los estudiantes implicados durante todo el tiempo, lo que les dio la posibilidad de hablar, de tratar otros temas, y de distraerse. Una sugerencia fue probar con alguna variante del juego del teléfono para que se llevase a cabo simultáneamente.
Cinco posibles extensiones:
- Se podría limitar el número de elecciones de la red permitidas, o no utilizar un listado y dejar que los participantes escriban los nombres de sus contactos de la red.
- Si se tiene contacto con la clase antes del ejercicio programado, se podría hacer la encuesta antes del encuentro.
- Se podría variar el número de adoptantes iniciales, los nodos de partida, para ver cómo afecta a la difusión.
- Se podrían utilizar diferentes fichas para representar los rumores, la desinformación o innovaciones competidoras. Quizá serviría para modelar situaciones de difusión de la vida real de un modo más realista.
- Finalmente, en nuestro segundo día de ensayos, pude llevar a cabo juegos utilizando sólo lazos recíprocos, lo que redujo la red y acortó el tiempo requerido para alcanzar la saturación.
Referencias bibliográficas
Chaffee, S. H. & Roser, C. (1986). Involvement and consistency of knowledge, attitudes and behaviors. Communication Research, 13, 373-399.Hornik, R. (1989). The knowledge-behavior gap in public information campaigns: A development communication view. In C. T. Salmon (Ed.) Information Campaigns: Balancing social values and social change. Newbury Park, CA: Sage.
Pemberton, E. (1936). The curve of culture diffusion rate. American Sociological Review, 1, 547-556.
Rogers, E. M. (1995). Diffusion of innovations (4th edition). New York: The Free Press, pages 1-37.
Valente, T. W. (1993). Diffusion of innovations and policy decision-making. Journal of Communication, 43 (1), 30-45.
Valente, T. W. (1995). Network models of the diffusion of innovations. Cresskill, NJ: Hampton Press.
Westoff, C. F. (1988). Is de KAP-gap real? Population and Development Review, 14 (2), 225-232.
Apéndice
Comunicación interpersonal
Este cuestionario se utilizará para demostrar cómo las redes interpersonales canalizan la difusión. Por favor, sigue las instrucciones respondiendo a las siguientes cuestiones:
- Por favor, señala con un círculo tu nombre en la lista de nombres de la primera columna. Si no aparece tu nombre, escríbelo al final de la lista y díselo al profesor.
- En la columna 2, señala con una “X” los nombres de aquellos con los que pasas tu tiempo libre fuera de la escuela (tus amigos).
- En la columna 3, señala con una “X” los nombres de aquellos con los que has ido a comer en los últimos tres meses.
- En la columna 4, señala con una “X” los nombres de aquellos con los que hablas de temas de salud.
- En la columna 5, señala con una “X” los nombres de aquellos a los que solicitas consejo sobre temas académicos.
| # |
Nombre |
Tiempo libre |
Comer |
Salud |
Consejo académico |
| 1 |
Nombre 1 |
||||
| 2 |
Nombre 2 |
||||
| 3 |
Nombre 3 |
||||
| |
|||||
| 31 |
Nombre 31 |
||||
| 32 |
Nombre 32 |
||||
[Nota: se dejan filas en blanco al final para hacer añadidos a la lista]
Reglas del juego de la red de difusión
(La brecha CAP)
Las reglas son:
- Sólo puedes darle una ficha a aquellos que te han nominado (se refieren a tu nombre en el listado).
- Sólo puedes dar fichas a otros al comienzo de un turno. (En otras palabras, no puedes conseguir una ficha en una “vuelta” y dársela inmediatamente a alguien).
- Sólo puedes dar una ficha de un color a una persona en un momento, pero puedes dar fichas a tantas personas como estés conectado y puedes darle a la misma persona fichas de diferentes colores.
Por ejemplo, si yo tengo tres fichas blancas, dos azules y una roja pueda dar dos blancas a dos personas diferentes y una azul.
- Para recibir una ficha azul debes tener primero una blanca. Para recibir una ficha roja debes tener primero una azul.
- La primera vez que consigas una ficha de un color, coloca un “punto” de ese color en tu hombro izquierdo.
Reglas del juego de la red de difusión
(Modelo del líder de opinión)
Las reglas son:
- Sólo puedes darle una ficha a aquellos que te han nominado (se refieren a tu nombre en el listado).
- Se dan fichas a otros sólo al comienzo del turno. (En otras palabras, no se puede pasar inmediatamente la ficha que has recibido en un turno).
- Sólo puedes dar una ficha de un color a una persona a la vez, pero puedes dar fichas a tantas personas como estés conectado, y puedes darle a la misma persona fichas de diferentes colores.
Por ejemplo, si tengo tres fichas blancas, dos azules y una roja, puedo pasar dos blancas a dos personas diferentes, y una azul.
- La primera vez que consigas una ficha de un color, coloca un “punto” de ese color en tu hombro izquierdo.
Juego 1, Ensayo 1: Ejercicio del líder de opinión.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Líderes (rojo) |
||||||||
| Aleatorios (blanco) |
||||||||
| Marginales (azul) |
||||||||
Juego 1, Ensayo 2: Ejercicio del líder de opinión.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Líderes (rojo) |
||||||||
| Aleatorios (blanco) |
||||||||
| Marginales (azul) |
||||||||
Juego 1, Ensayo 3: Ejercicio del líder de opinión.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Líderes (rojo) |
||||||||
| Aleatorios (blanco) |
||||||||
| Marginales (azul) |
||||||||
Juego 2, Ensayo 1: Ejercicio de la brecha CAP con iniciadores aleatorios.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Conocimiento (rojo) |
||||||||
| Actitud (blanco) |
||||||||
| Práctica (azul) |
||||||||
Juego 2, Ensayo 2: Ejercicio de la brecha CAP con iniciadores aleatorios.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Conocimiento (rojo) |
||||||||
| Actitud (blanco) |
||||||||
| Práctica (azul) |
||||||||
Juego 2, Ensayo 3: Ejercicio de la brecha CAP con iniciadores aleatorios.
| Etapa |
Tiempo |
|||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| Conocimiento (rojo) |
||||||||
| Actitud (blanco) |
||||||||
| Práctica (azul) |
||||||||