Introducción al análisis de datos reticulares
Prácticas
con UCINET6 y NetDraw1
Versión
1
Águeda Quiroga
Departamento de Ciencias Políticas, Universidad
Pompeu Fabra
Junio 2003
UCINET 6 for Windows
Version
6.26 / 30 May 2003
Copyrigt
© 1999-2003 Analytic Technologies
Borgatti,
S.P., M.G. Everett, and L.C. Freeman. 2002. UCINET
6 for Windows Software for Social Network Analysis. Harvard: Analytic Technologies
Puede obtenerse una versión de evaluación
gratuita en: http://www.analytictech.com/downloaduc6.htm
NetDraw1.0:
Copyright 2002 Steve Borgatti
Contenidos
Introducción 4
Sobre el análisis de redes sociales 5
Descripción del ejercicio práctico 7
Crear una matriz con UCINET 6 9
Graficar una matriz con NetDraw1 17
Medidas de centralidad 28
Rango
(degree) 28
Grado
de intermediación (betweenness) 34
Cercanía
(closenness) 37
Conclusiones 43
Introducción
Este manual tiene como objetivo introducir conceptos básicos del
análisis de datos reticulares (o análisis de redes sociales), utilizando
herramientas de análisis y representación de datos, como UCINET 6 y NetDraw1.
Se trata de un texto orientado hacia la puesta en práctica de estos
conceptos iniciales, a través de la realización de un ejercicio práctico.
Los contenidos de este manual surgen de tres fuentes principales:
-
Hanneman, Robert, Introducción a los métodos de análisis de redes
sociales
-
Molina, José Luis, El análisis de redes sociales. Una
introducción
-
Wasserman, S. y Faust, K., Social Network Análisis. Methods and applications.[1]
Y conforman una breve introducción al análisis de redes sociales, al
tipo de datos que se utilizan en dicho análisis y a su correcto tratamiento. A
lo largo del ejercicio se construyen matrices, se grafican y analizan los datos
a través de tres medidas de centralidad: rango, grado de intermediación y grado
de cercanía.
Sobre el análisis de
redes sociales
¿Qué es el análisis de redes sociales? Veamos una definición:
“El análisis de redes sociales se ocupa del estudio
de las relaciones entre una serie definida de elementos (personas, grupos,
organizaciones, países e incluso acontecimientos). A diferencia de los análisis tradicionales
que explican, por ejemplo, la conducta en función de la clase social y la
profesión, el análisis de redes sociales se centra en las relaciones y no en
los atributos de los elementos”. (Molina, op.cit: p. 13)
La particularidad del análisis de redes sociales radica entonces en el
énfasis en las relaciones entre los elementos estudiados, entre sus propiedades
relacionales, y no en las características monádicas (atributos individuales) de
cada elemento (aunque los datos atributivos también pueden ser incorporados en
el análisis, como veremos más adelante).
Como señala Hanneman (op.cit), los datos sociológicos “tradicionales” se
representan en una matriz rectangular en donde se inscriben las mediciones. En
las filas se ubican los casos u observaciones (personas, organizaciones, países,
etc.), y en las columnas, las variables seleccionadas (edad, tipo de organización,
población, etc.). En cambio, en el análisis de redes sociales
“los
datos de la ‘red’ (en su forma más pura), constituyen una matriz cuadrada de
mediciones. Las filas de la matriz son los casos, sujetos u observaciones. Las
columnas son el mismo conjunto de casos, sujetos y observaciones –allí está la
diferencia clave con los datos convencionales. En cada celda de la matriz se
describe una relación entre los actores”. (p. 5)
Figura 1. Matriz con
datos sociológicos “convencionales”
|
Informante |
Edad |
Sexo |
Ocupación |
|
FFG |
32 |
Mujer |
Secretaria
administrativa |
|
BNM |
20 |
Hombre |
Estudiante |
|
DFP |
45 |
Hombre |
Funcionario público |
|
CCD |
37 |
Mujer |
Abogada |
|
STR |
26 |
Mujer |
Docente |
Figura 2. Matriz con
datos relacionales
|
¿Quién es amigo de quién? |
|||||
|
|
FFG |
BNM |
DFP |
CCD |
STR |
|
FFG |
- |
1 |
0 |
0 |
1 |
|
BNM |
1 |
- |
1 |
0 |
0 |
|
DFP |
0 |
1 |
- |
1 |
1 |
|
CCD |
0 |
0 |
1 |
- |
0 |
|
STR |
1 |
0 |
1 |
0 |
- |
En las figuras 1 y 2 se presenta un ejemplo de los dos tipos de matrices
señaladas por Hanneman. La primera se fija en las características de los
individuos. La segunda, en las relaciones que mantienen dichos individuos entre
sí. Así, se ha marcado con 1 la presencia de la relación de amistad y con 0 su
ausencia.
Los elementos básicos del análisis de redes sociales son, entonces,
los nodos (los puntos que representan a personas, grupos, países, etc.) y la
relación o vínculo que nos interesa analizar (amistad, enemistad, parentesco,
comercio, etc.) y que se establece entre tales nodos.
Descripción del
ejercicio práctico
A lo largo de este manual trabajaremos con un ejemplo sencillo, a fin
de introducir las herramientas básicas. Analizaremos las relaciones de
conocimiento de un curso de estudiantes universitarios. Contamos con el listado
de estudiantes (nombre y sexo) y la carrera a la que pertenecen. Además, cada
uno de ellos ha respondido un cuestionario en el que se les preguntaba a
quiénes de los demás integrantes de la clase conocían personalmente antes de
iniciar el curso.
Así, los nodos serán en este caso los estudiantes, y el vínculo a
analizar será la relación de conocimiento previo. Conviene precisar bien a qué
propiedad relacional nos referimos. No se trataba en este caso de preguntar
quiénes eran amigos de quiénes, ni de si algún estudiante tenía conocimiento
indirecto de otro (ambos casos resultan problemáticos por diversas razones). Se
trata de la propiedad “conocer a”, que en nuestro estudio (y en el
cuestionario) se entendía como tener un mutuo conocimiento personal (que no
tiene por qué implicar relación continuada, pero sí alguna interacción pasada).
Con los datos de las tablas 1 y 2 elaboraremos las matrices que utilizaremos
para el análisis
Tabla 1. Listado de
estudiantes
|
Nombre |
Sexo (M/F) |
Carrera |
|
Andrés |
M |
Antropología |
|
Carlos |
M |
Arqueología |
|
Carme |
F |
Arqueología |
|
Carmen |
F |
Antropología |
|
Carol |
F |
Arqueología |
|
Dolors |
F |
Antropología |
|
Hugo |
M |
Sociología |
|
Joan |
M |
Antropología |
|
José |
M |
Psicología Social |
|
Julio |
M |
Antropología |
|
Liliana |
F |
Sociología |
|
María |
F |
Psicología Social |
|
Mariano |
M |
Arqueología |
|
Martha |
F |
Arqueología |
|
Nuria |
F |
Psicología Social |
|
Pau |
M |
Antropología |
|
Xavi |
M |
Psicología Social |
Tabla 2. Resultado del
cuestionario
|
Nombre |
Conoce a |
|
Andrés |
Carlos, Carmen, Dolors,
Joan, Julio, Pau |
|
Carlos |
Carme, Carol, Andrés |
|
Carme |
Carlos, Carol |
|
Carmen |
Andrés, Dolors, Pau |
|
Carol |
Carlos, Carme |
|
Dolors |
Andrés, Carmen, José |
|
Hugo |
Liliana |
|
Joan |
Andrés, Julio, Pau,
José |
|
José |
Dolors, Joan, María,
Nuria, Xavi |
|
Julio |
Andrés, Joan |
|
Liliana |
Hugo |
|
María |
José, Nuria, Xavi |
|
Mariano |
Martha, Pau |
|
Martha |
Mariano, Pau |
|
Nuria |
José, María |
|
Pau |
Andrés, Carmen, Joan,
Martha, Mariano |
|
Xavi |
José, María |
Crear una matriz con
UCINET 6
El primer paso en nuestro análisis de redes del ejemplo planteado
consiste en construir una matriz con la información de que disponemos, a fin de
poder analizarla y graficarla. Para eso, utilizaremos el programa UCINET 6.
Al iniciar dicho programa UCINET 6 nos encontramos con la siguiente
pantalla:
Figura 3
Al operar en un entorno Windows, el programa presenta características
comunes a los programas elaborados para este sistema operativo. Cuenta con una
barra de menús desplegables (File, Data, Transform, Tools, Network, Draw,
Options, Help) más una serie de iconos de acceso directo. Si nos fijamos en la
figura 3, veremos que en el centro de la barra de trabajo hay un rectángulo
blanco, donde se lee “C:\archivos de programa\Ucinet6\manual. Esta dirección
nos indica el directorio en el que estamos trabajando, y en el que por defecto
guardará los archivos. Para definir otra carpeta o directorio se debe hacer
click en el icono de la derecha del rectángulo, que abrirá una ventana con las
opciones.
Nuestra primera tarea es, como hemos dicho, crear una matriz en la
cual almacenar la información que de que disponemos en la tabla 2.
Para eso activaremos la función “Spreadsheet” (el segundo icono desde
la izquierda):
Figura 4
Al activarlo, se abre la pantalla que nos permitirá introducir los
datos en la matriz. Como podemos observar en la figura 5, se trata de un
formato similar al de una hoja de cálculo.
Figura 5
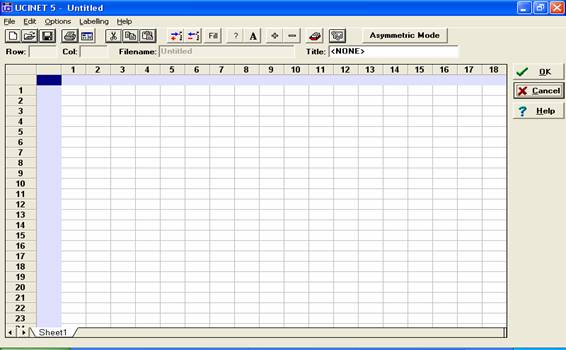
En el extremo derecho de la barra de tareas se encuentra un botón con
la leyenda “Asymmetric Mode”. Como su nombre lo indica, significa que la matriz
está preparada para introducir datos no simétricos, es decir datos en los que
el vínculo va en una sola dirección. Por ejemplo, este sería el caso si
estuviéramos analizando la relación “Prestar dinero a”. Que A preste dinero a B
no implica que B preste dinero a A. Es una relación no simétrica. Por el
contrario, la relación que analizamos en este ejemplo sí es simétrica. Que A
conozca a B implica que B conoce a A. Por lo tanto, al ingresar un valor para
la relación entre A-B, se repite el mismo valor para la relación B-A.
Recordemos que cuando precisábamos el significado de la propiedad relacional
“conocer a”, afirmamos que evitábamos en este caso hacer referencia a otras
propiedades como la de la amistad, que puede resultar un caso dudoso entre
relación simétrica y asimétrica. Pero, en nuestro caso, y tal y como ha sido
definida la propiedad, no cabe duda de que la relación “conocer a” es
simétrica.
Antes de continuar con la introducción de datos en la matriz es
conveniente realizar una aclaración sobre los tipos de vínculos. Los lazos o
vínculos pueden ser orientados o no orientados, según los ejemplos mencionados
en el párrafo anterior (conocimiento como una relación no orientada, prestar
dinero como una relación orientada). Pero, por otra parte, también pueden ser o
binarios o ponderados. Son binarios cuando medimos la ausencia o presencia de
la relación. En el caso que estamos analizando, si dos personas se conocen
previamente le damos el valor 1 y si no, 0. Pero también podríamos querer
valorar el tipo de relación que tienen dos personas, ponderando el vínculo, por
ejemplo, entre 0 si no hay conocimiento, 1 si son apenas conocidos, 2 si son conocidos
con una relación continuada, 3 si son amigos y 4 si son amigos muy cercanos. A
lo largo de este ejemplo sólo trabajaremos con vínculos no orientados y binarios,
pero es importante recordar que se pueden utilizar también vínculos orientados
y vínculos ponderados, y que dentro de estos existe una gran pluralidad
variantes.[2]
Dado que, como hemos dicho, en nuestro ejemplo los vínculos no son
orientados, cambiaremos la función a “Symmetric Mode”. Al hacer click en el
botón “Assymetric Mode” cambia el modo de la matriz:
Figura 6
Introduciremos a continuación los encabezados de las filas y las
columnas. Al ser una matriz de modo simétrico, al ingresar un nombre en una
fila completará el nombre en la columna correspondiente al mismo tiempo. Para
ingresar los nombres, simplemente lo escribimos en la celda coloreada que se
encuentra al costado de cada número, en las filas o debajo, en las columnas.
Una vez introducido, apretamos la tecla “Enter”:
Figura 7
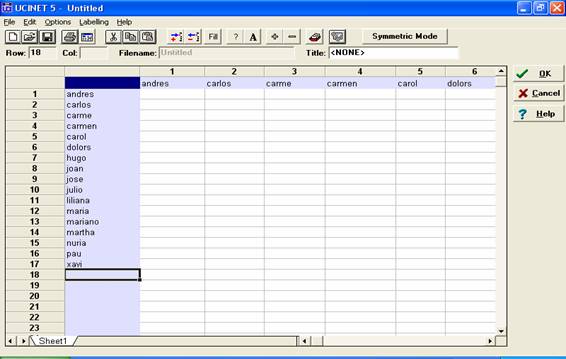
Hemos introducido ya los nodos de la red que queremos analizar. A
continuación introduciremos los valores de la relación. Así, sobre la base de
los datos de la tabla 2, volcaremos la información correspondiente a cada par
de personas. Introduciremos un 1 si hay relación y dejaremos la celda en blanco
si no la hay:
Figura 8
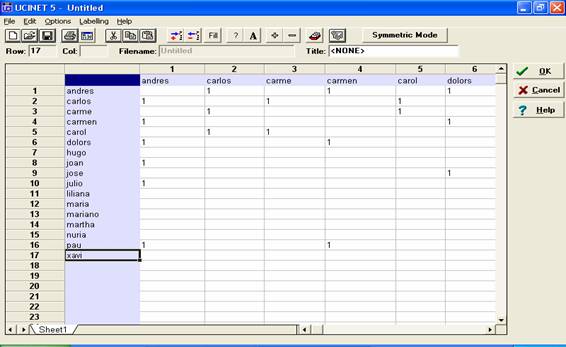
Una vez completa nos ubicaremos en la última celda (en este caso, en
la intersección de la columna 17 con la fila 17) y desde allí haremos click con
el ratón en el icono “fill”. De esta manera, se completarán con ceros el resto
de las celdas de la matriz:
Figura 9
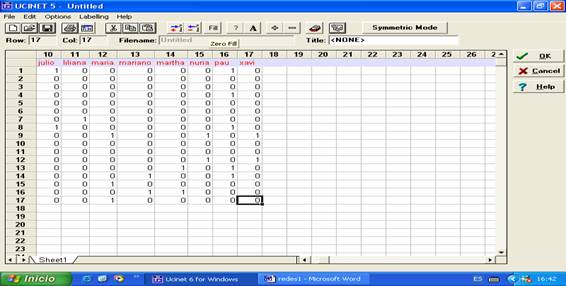
Hemos completado así la matriz con las relaciones. La guardaremos con
el nombre “estudiantes” (a partir del menú File< save as<).
A continuación crearemos dos nuevas matrices, en las que almacenaremos
los datos atributivos de la tabla 1 (sexo y carrera a la que pertenecen los
estudiantes). Recordemos que los datos atributivos son propiedades
individuales, y por lo tanto no relacionales, de los nodos que son objeto de
nuestro análisis. Para ellos, abriremos la matriz que acabamos de crear
(File< open < estudiantes.##h) y realizaremos nuevamente la operación
“save as”. Llamaremos “carrera” a este nuevo fichero ( File< save as<
carrera).
Introduciremos en esta matriz (carrera.##h) los datos correspondientes
a la carrera universitaria que estudian los alumnos de la clase. Para
aprovechar el listado de los nombres, eliminaremos la información de las
columnas. Seleccionamos con el ratón las 17 columnas y apretamos la tecla
“Suprimir” o “Delete”:
Figura 10
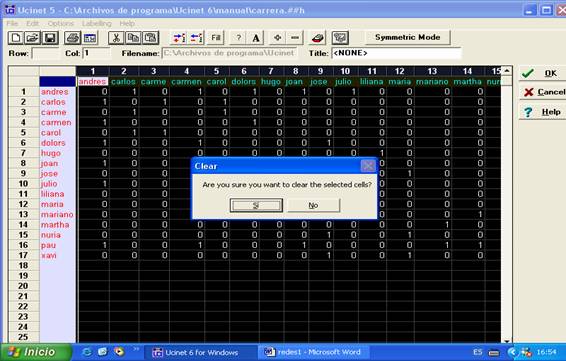
Una vez borrada la información de las columnas, cambiaremos el modo de
la matriz a “Asymmetric Mode” (esta matriz ya no será cuadrada como la
anterior, sino que tendrá 17 filas y 1 columna). Escribimos en el encabezado de
la columna 1 (en la zona coloreada debajo del número 1) “carrera” (sin las
comillas). Introduciremos en esa columna la información codificada de la
siguiente manera: 1 para los estudiantes de antropología, 2 para los de
arqueología, 3 para los de sociología y 4 para los de psicología social:
Figura 11
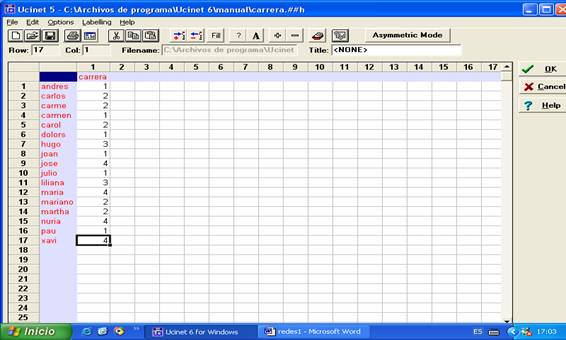
Guardamos la matriz (click en el botón “OK”). Elegimos “yes” en la
opción guardar cambios:
Figura 12
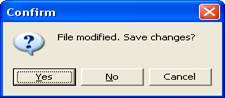
A continuación, abrimos la matriz que acabamos de crear (File<
open< carrera.##h) y la guardamos con el nombre “sexo” (File< save as<
sexo). Realizamos sobre esta matriz la misma operación que en el caso anterior
(borramos la columna 1) y escribimos como encabezado de la misma “sexo” (sin
comillas) e introducimos la información codificada de la siguiente manera: 1
para varones y 2 para mujeres:
Figura 13
Cerramos la matriz (click en botón “Ok”) y guardamos los cambios.
Hemos ingresado ya toda la información que utilizaremos.
Graficar una red con
NetDraw1
A continuación, veremos la representación gráfica de la primera matriz
que hemos creado, la que resume la información sobre las relaciones existentes
entre los estudiantes.
Una vez cerrada la función “Spreadsheet”, regresamos a la pantalla
inicial de UCINET 6. Allí hacemos un click sobre el icono que abre el programa
NetDraw (el séptimo icono contando desde la izquierda):
Figura 14
Se abre así una ventana con el programa NetDraw. Este programa se
utiliza para visualizar gráficamente redes sociales. Veremos representada en
grafos la matriz que hemos introducido. Para ello, abriremos la matriz
“estudiantes.##h” que hemos creado anteriormente. Hacemos click en el icono
“open ucinet network dataset” (el segundo desde la izquierda)
Figura 15
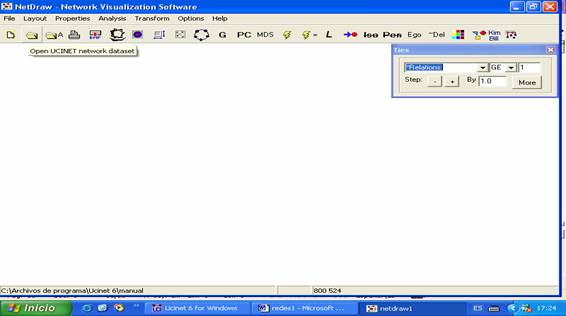
Elegimos la matriz con la que trabajaremos (estudiantes.##h):
Figura 16
Al abrirla obtenemos el siguiente gráfico:
Figura 17
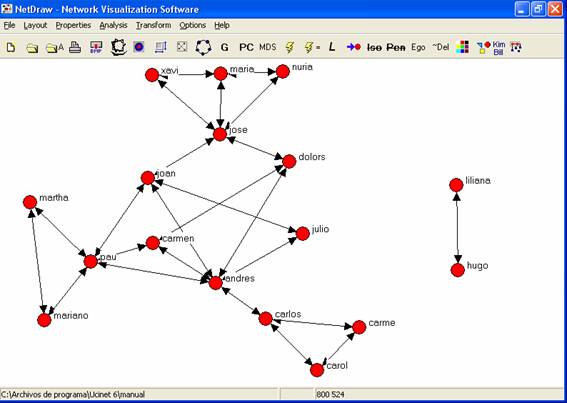
Vemos representadas gráficamente las relaciones que habíamos
introducido en la matriz. Así, por cada par de personas que habíamos conectado
en la matriz (mediante el 1 que señalaba la relación) observamos un vínculo que
une los dos nodos. Como se trata de una relación no orientada, cada grafo tiene
una doble flecha (Hugo conoce a Liliana y Liliana conoce a Hugo). Un grafo no
orientado también se representa como un segmento que une dos nodos, sin ninguna
flecha que indique dirección.
Esta red sociométrica[3]
nos presenta una fotografía de las relaciones que existen al interior de un
grupo (la clase, en este caso). A simple vista podemos observar que existen
individuos más conectados que otros, que existen sub-grupos dentro de la red,
etc. Podríamos entonces intentar establecer hipótesis acerca de las relaciones
existentes. Por ejemplo, podríamos inducir que las personas que cursan las
mismas carreras se relacionan más entre sí que las de carreras diferentes. Para
ello, necesitamos complementar la información con los datos atributivos que
hemos recopilado.
Para ello, superpondremos la matriz que contiene la información sobre
las carreras a la matriz que representaba las relaciones de conocimiento y que
ya hemos realizado. La operación es muy sencilla. Abrimos la matriz de atributos
(haciendo click en el tercer icono desde la izquierda “open UCINET attibute
dataset”) y seleccionamos el fichero “carrera.##h”:
Figura 18
A continuación introduciremos los atributos en la red, haciendo click
sobre el cuarto icono de la barra de tareas, contando desde la derecha:
Figura 19
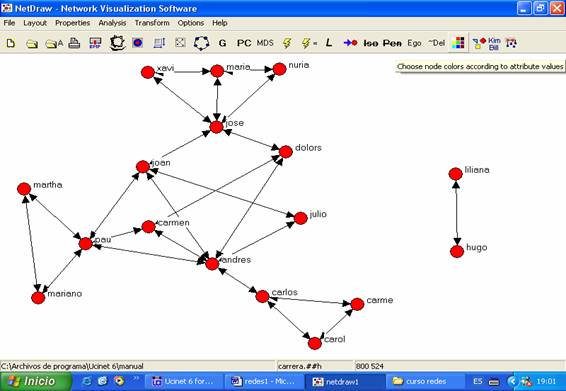
Se desplegará una nueva pantalla, en la que seleccionaremos el
atributo “carrera”:
Figura 20
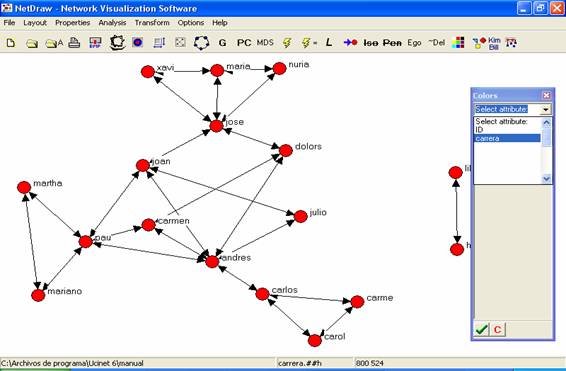
Veremos los cuatro códigos que hemos introducido para las carreras,
cada uno de ellos asociado a un color diferente. Si quisiéramos cambiar el
color adjudicado a alguno, sólo hay que hacer click sobre el rectángulo de
color que se encuentra a la izquierda del código y seleccionar el color que
deseamos en la paleta que se despliega. En este caso, cambiaremos el color
correspondiente al código 2, de negro a verde:
Figura 22
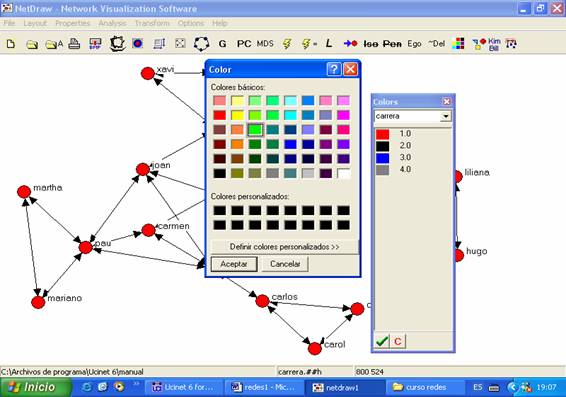
Una vez efectuado el cambio, hacemos click sobre el botón “Aceptar”.
Vemos entonces que a cada persona le corresponde el color de la carrera que
está estudiando: rojo para antropología, verde para arqueología, azul para
sociología y gris para psicología social.
Figura
23
A continuación, introduciremos los datos correspondientes al sexo,
utilizando formas diferentes para los nodos, según representen hombres o
mujeres. Introducimos entonces la matriz correspondiente al sexo (icono de
datos atributivos, presentado en la figura 18), sexo.##h. Y seleccionamos la
función “Choose node shapes according to attribute values” (tercer icono
contando desde la izquierda):
Figura 24
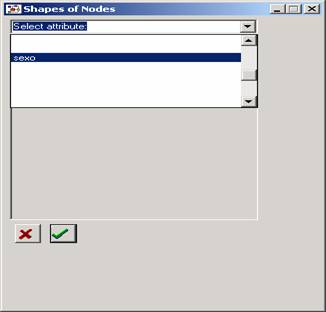
Se abrirá una ventana similar a la que utilizamos para definir los
colores. Seleccionamos el atributo “sexo”. Un consejo: si en el menú
desplegable (“select attibute”) no vemos el atributo que queremos introducir, debemos
descender hacia el final de la ventana, hasta encontrarlo.
Figura 25
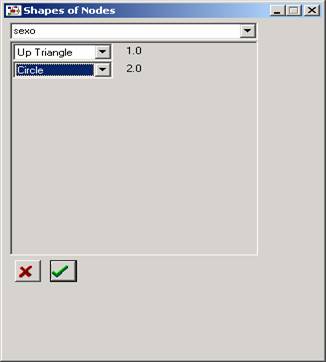
A continuación seleccionaremos un triángulo para identificar a los hombres (codificados con el valor “1”) y un círculo para identificar a las mujeres (codificadas con el valor “2”):
Figura
26
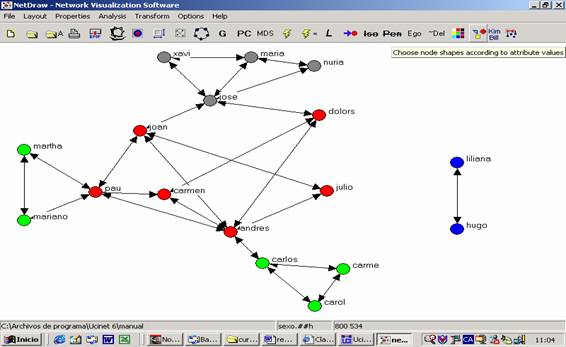
De esta manera hemos introducido los dos atributos en la red. Y obtenemos el siguiente resultado:
Figura 27
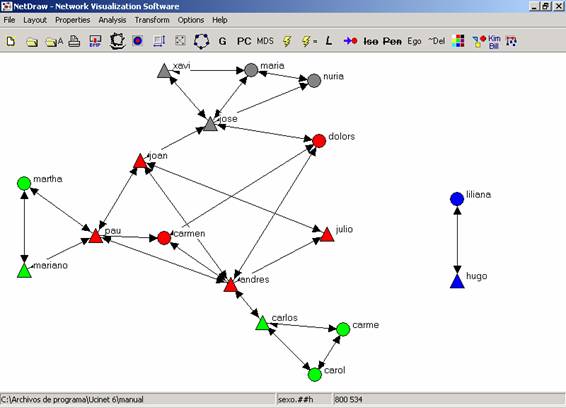
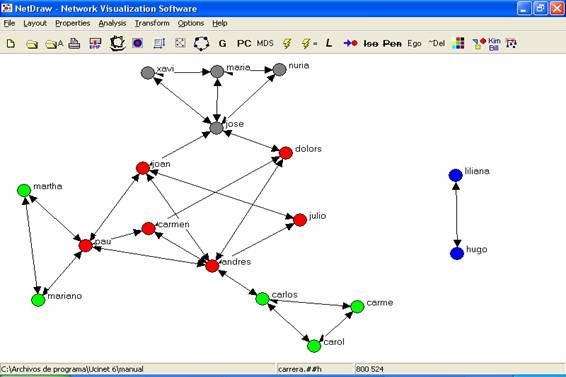
Hemos conseguido una
descripción más detallada de la red de interacciones. Como podemos observar en
la figura 27, existen sub-grupos en el interior de nuestra red, y personas con
más conexiones que otras. Así, los que cursan la carrera de antropología
(marcados en rojo) se conocían todos entre sí antes de iniciar el curso. Lo
mismo pasa con los estudiantes de psicología social (nodos grises) y los de
sociología (nodos azules). Sin embargo, no sucede lo mismo con los estudiantes
de arqueología (verde), entre los que podemos observar dos grupos
diferenciados. Por el contrario, no parece haber ningún patrón diferenciado de
relación entre hombres y mujeres.
En lo que hace a las
personas, algunos estudiantes sólo conocen a una o dos personas del grupo,
mientras que otras (como Andrés o Joan) conocen a mucha gente. Pero para saber
con certeza cuáles son las características de esta red, recurriremos al cálculo
de las medidas de centralidad, a fin de realizar una primera aproximación al
análisis de esta red social. Antes de pasar a esta sección, exportaremos la
imagen de la red que hemos obtenido, para poder utilizarla posteriormente. Para
ello, desde la función “File” de la barra de menús seleccionamos la función
“Save diagram as” y luego el formato que elijamos (en este caso, “Bitmap”)
Figura 28
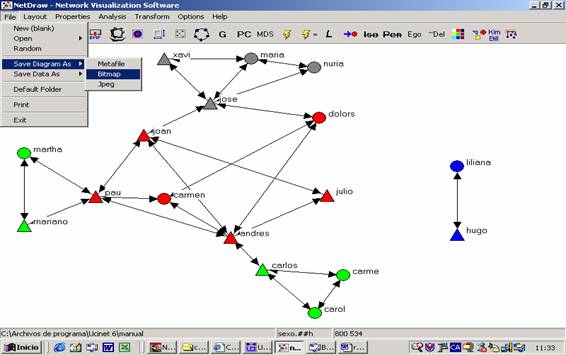
La guardaremos con el nombre
“redestudiantes”. Para concluir la primera parte de la práctica, crearemos un
documento en Word (con el nombre “informe práctica.doc”), e insertaremos la
imagen que hemos creado (Insertar < imagen< desde archivo):
Figura 29
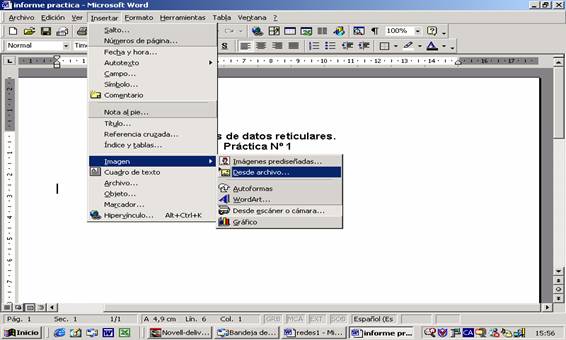
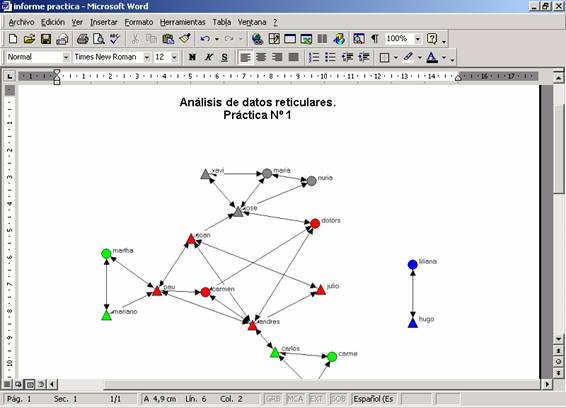
Seleccionamos la imagen a insertar (“redestudiantes”), y guardamos los
cambios realizados en el informe:
Figura 30
Medidas de centralidad
Como señala Hanneman (op.cit.),
La perspectiva de redes implica tener en cuenta múltiples niveles de análisis. Las diferencias entre los actores son interpretadas en base a las limitaciones y oportunidades que surgen de la forma en que éstos están inmersos en las redes; la estructura y el comportamiento de las redes está basado en y activado por las interacciones locales entre los actores. (...) Las diferencias en cómo los individuos están conectados puede ser extremadamente útil para entender sus atributos y comportamiento. Muchas conexiones significan a menudo que los individuos se exponen todavía a más y más diversa información. (cap V: p. 3)
Podemos realizar una primera aproximación a la estructura de una red
social mediante el análisis de tres medidas de centralidad: rango (degree), grado de intermediación (betweenness) y cercanía (closeness). Por medida de centralidad se
entiende un conjunto de algoritmos calculado sobre cada red que nos permite
conocer la posición de los nodos en el interior de la red y la estructura de la
propia red. Veamos qué significa cada una de estas medidas, cómo se calculan y
cómo se interpretan.
Rango (degree)
El rango es el número de lazos directos de un actor (o nodo), es decir
con cuántos otros nodos se encuentra directamente conectado. Si volvemos a la
figura 23, por ejemplo, podemos observar que Martha está conectada a dos
personas: Mariano y Pau. Su rango, entonces es 2. Andrés, en cambio, conoce a
seis personas: su rango es 6. En este caso es sencillo calcularlo a simple
vista. Pero para trabajar con mayor precisión, utilizaremos UCINET 6. Desde el
menú “Network” seleccionaremos la función “Centrality” y luego “Degree”:
Figura 31
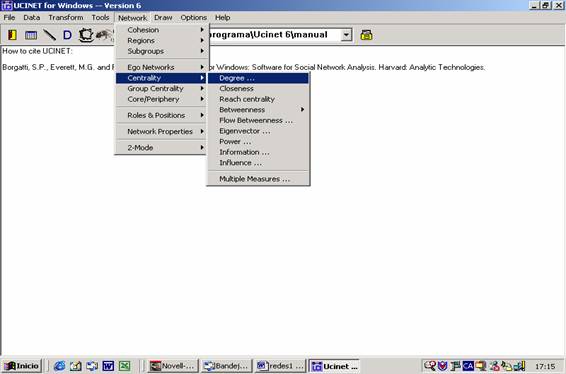
En la pantalla que se despliega seleccionaremos la matriz que contiene
los datos que queremos analizar. En este caso, analizaremos la matriz
“estudiantes.##h”, la que contiene la información sobre las relaciones de
conocimiento entre los estudiantes de la clase. Para ello, haremos click con el
ratón en el botón de la fila “imput dataset” (marcado con tres puntos):
Figura 32
Una vez seleccionada la matriz obtenemos la siguiente pantalla:
Figura 33
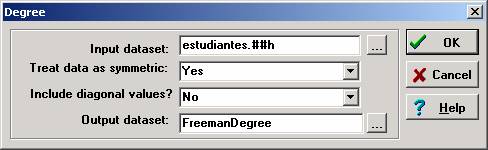
La primera fila (“Input dataset”) indica el fichero que utilizará para
calcular el rango. La segunda fila (“Treat data as symmetric”) pregunta si se
trata de una matriz simétrica (la relación de A-B vale para B-A) o no. En este
caso, la respuesta es “sí”. La tercera fila (Include diagonal values?) pregunta
si debe tener en cuenta los valores de la diagonal (la relación entre A y A, B
y B, C y C, etc.), y responderemos “no”. La cuarta fila informa con qué nombre
se guardarán los resultados, en el directorio que tengamos predeterminado.
Haciendo click en el icono de los tres puntos, se puede definir otro directorio
y modificar el nombre del archivo con los datos de salida si así lo deseamos.
Una vez realizados los cambios que queremos hacer, hacemos click en “aceptar”.
Obtenemos la siguiente pantalla:
Figura 34
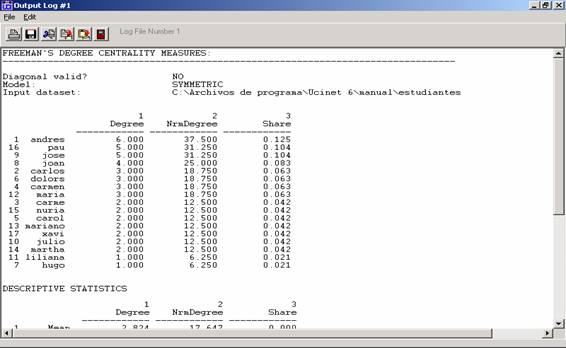
Vemos la lista de todos los nodos de la red, ordenados de mayor rango
(más número de conexiones) a menor rango (menor número de conexiones). Se
reproduce a continuación la información obtenida en las tres primeras columnas:
Tabla 3
|
|
Degree |
NrmDegree |
|
Andrés |
6.0 |
37.500 |
|
Pau |
5.0 |
31.250 |
|
José |
5.0 |
31.250 |
|
Joan |
4.0 |
25.000 |
|
Carlos |
3.0 |
18.750 |
|
Dolors |
3.0 |
18.750 |
|
Carmen |
3.0 |
18.750 |
|
María |
3.0 |
18.750 |
|
Carme |
2.0 |
12.500 |
|
Nuria |
2.0 |
12.500 |
|
Carol |
2.0 |
12.500 |
|
Mariano |
2.0 |
12.500 |
|
Xavi |
2.0 |
12.500 |
|
Julio |
2.0 |
12.500 |
|
Martha |
2.0 |
12.500 |
|
Liliana |
1.0 |
6.250 |
|
Hugo |
1.0 |
6.250 |
La columna “Nrmdegree” indica el rango normalizado, es decir, el
porcentaje de conexiones que tiene un nodo sobre el total de la red.
El análisis del rango nos indica que la persona más conectada en este
grupo, la de mayor centralidad, es Andrés, y que Liliana y Hugo son los menos
centrales, con un rango de 1 cada uno. Podríamos suponer que Andrés es la
persona que controla mayor cantidad de información. El rango puede ser
considerado una medida que permite acceder al índice de accesibilidad a la
información que circula por la red. Si, por ejemplo, en el interior del grupo
circularan ciertos rumores, los actores con un rango más alto tendrán mayores
probabilidades de escucharlos y difundirlos. El rango también puede ser
interpretado como el grado de oportunidad de influir o ser influido por otras
personas en la red.[4]
Pongamos por ejemplo el caso de la red que estamos analizando. Supongamos que
nos interesa realizar algunas modificaciones en el dictado de la asignatura o
que queremos conocer la valoración de los estudiantes sobre su desarrollo. En
este caso Andrés (con un rango de 6, el más alto de la red) parece ser un buen
informante, alguien que tiene acceso a bastante información de la que circula
por el grupo. Podemos utilizar el rango también, por ejemplo, como un método de
selección de personas para entrevistas o negociaciones.
Pero debemos complementar este análisis con las otras medidas de
centralidad, para obtener un panorama más completo. Antes de hacerlo, nos
referiremos a los estadísticos descriptivos que acompañan la información:
Figura 35
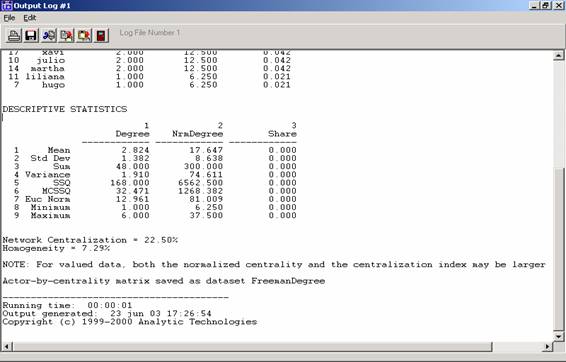
Los estadísticos descriptivos brindan información sobre los valores
que tomó el rango en el conjunto de la red. Vemos que el rango promedio de la
red (“Mean”) es 2.824, y que los valores oscilan entre 1 y 6 (la menor y mayor
cantidad de lazos).
Incorporaremos esta información al informe de la práctica, de manera
muy sencilla: seleccionamos con el ratón el texto y seleccionamos la función
“copiar” (Edit< copy). Pegamos la información en el informe en Word que
estamos elaborando (Edición< pegar).
Figura 36
Grado de intermediación (betweenness)
El grado de intermediación indica la frecuencia con que aparece un
nodo en el tramo más corto (o geodésico) que conecta a otros dos. Es decir,
muestra cuando una persona es intermediaria entre otras dos personas del mismo
grupo que no se conocen entre sí (lo que podríamos denominar “persona puente”).
Veamos cuáles son los valores para el grado de intermediación en nuestra red
para localizar un ejemplo.
Para calcular el grado de intermediación seleccionamos el menú Network<
Centrality< betweenness< nodes:
Figura 37
En la pantalla que se despliega elegimos la matriz que contiene los
datos que vamos a analizar (“estudiantes.##h”) y hacemos click en el botón
“ok”:
Figura 38

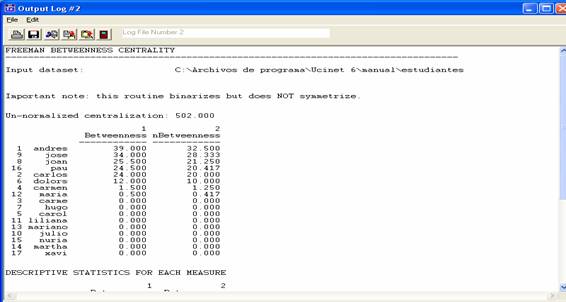
Obtenemos como resultado el valor del grado de intermediación de cada
nodo, ordenados de mayor a menor:
Figura 39
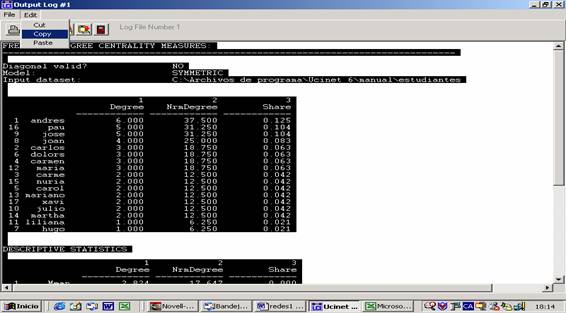
Se reproducen a continuación los resultados obtenidos:
Tabla 4
|
|
Betweenness |
nBetweenness |
|
Andrés |
39.0 |
32.5 |
|
José |
34.0 |
28.3 |
|
Joan |
25.5 |
21.2 |
|
Pau |
24.5 |
20.4 |
|
Carlos |
24.0 |
20.0 |
|
Dolors |
12.0 |
20.0 |
|
Carmen |
1.5 |
10.0 |
|
María |
0.5 |
1.2 |
|
Carme |
0.0 |
0.4 |
|
Hugo |
0.0 |
0.0 |
|
Carol |
0.0 |
0.0 |
|
Liliana |
0.0 |
0.0 |
|
Mariano |
0.0 |
0.0 |
|
Julio |
0.0 |
0.0 |
|
Nuria |
0.0 |
0.0 |
|
Martha |
0.0 |
0.0 |
|
Xavi |
0.0 |
0.0 |
Andrés y José son las personas con un mayor grado de intermediación.
Si observamos la figura 23 vemos que Andrés es la persona que conecta al grupo
de los antropólogos con uno de los grupos de los arqueólogos (el formado por
Carlos, Carme y Carol) y José conecta al grupo de los estudiantes de psicología
social con los de antropología. Pero Joan, Pau y Carlos también tienen valores
altos de grado de intermediación. La relación entre Joan y Pau permite conectar
tres grupos: arqueólogos, antropólogos y psicólogos sociales. En el caso de
Carlos, su relación con Andrés vincula a Carol y Carme con un grupo mayor. Si
esa relación se rompiese, el grupo quedaría aislado.
Realizaremos la misma operación que en el caso del rango:
seleccionaremos los resultados obtenidos y con la función “copiar” (ver figura
36) incorporaremos la información en el documento del informe.
Cercanía (closenness)
El grado de cercanía indica la cercanía de un nodo respecto del resto
de la red. Representa la capacidad que tiene un nodo de alcanzar a los demás.
Veremos su interpretación a partir de un ejemplo.
Para calcularlo, procederemos de la misma manera que en las dos
medidas de centralidad anteriores, es decir, a partir del menú “Network”
(network< centrality< closenness):
Figura 40
Seleccionamos el archivo a analizar y damos click en el botón “ok”:
Figura 41
El resultado de la operación, al igual que en los casos anteriores, es
la lista ordenada de los valores de cercanía, y también el de su opuesto,
lejanía (farness):
Figura 42
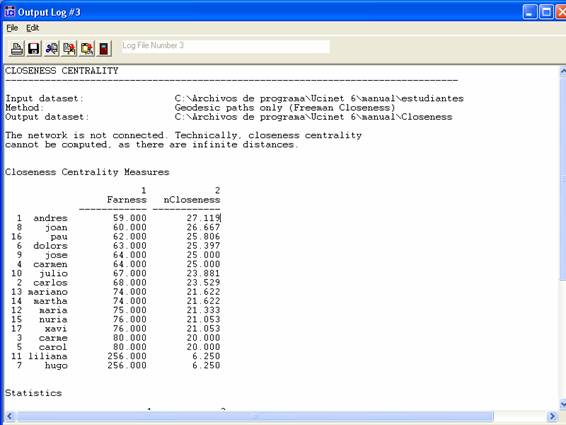
Se reproducen a continuación los resultados:
Tabla 5
|
|
Farness |
Closeness |
|
Andrés |
59.0 |
27.11 |
|
Joan |
60.0 |
26.66 |
|
Pau |
62.0 |
25.80 |
|
Dolors |
63.0 |
25.39 |
|
José |
64.0 |
25.00 |
|
Carmen |
64.0 |
25.00 |
|
Julio |
67.0 |
23.88 |
|
Carlos |
68.0 |
23.52 |
|
Mariano |
74.0 |
21.62 |
|
Martha |
74.0 |
21.62 |
|
Maria |
75.0 |
21.33 |
|
Nuria |
76.0 |
21.05 |
|
Xavi |
76.0 |
21.05 |
|
Carme |
80.0 |
20.0 |
|
Carol |
80.0 |
20.0 |
|
Liliana |
256.0 |
6.25 |
|
Hugo |
256.0 |
6.25 |
Al igual que en las dos medidas de centralidad anteriormente
analizadas, Andrés es la persona de la red que cuenta con un grado de cercanía
más grande. Tiene una mayor capacidad para acceder al resto de los nodos de la
red. Sin embargo, los resultados para el resto de las personas no son iguales a
los obtenidos en las mediciones anteriores. Si volvemos a los resultados de las
tabla 3, vemos que, por ejemplo, Dolors tenía el mismo rango que Carlos, Carmen
y María (conocían a tres personas cada uno). Sin embargo, el grado de cercanía
de Dolors es mayor que el de ellos. No sólo es importante el número de personas
que conoces, sino quiénes son esas personas, cuál es su grado de conexiones. Si
observamos la figura 23, vemos que Dolors conoce a Andrés y a José, las dos
personas con mayor grado de cercanía de toda la red. De esta manera, su
probabilidad de acceder al resto de los nodos es más alta. “[U]na persona poco
conectada con el resto (baja centralidad, bajo grado de intermediación) por el
solo hecho de estar conectada con una persona ‘importante’ puede tener una alta
cercanía” (Molina, op.cit: p. 79).
Finalizaremos ahora el ejercicio, copiando los resultados y
llevándolos al informe que hemos elaborado.
Conclusiones
En esta introducción al análisis de redes sociales se han mostrado los
principales conceptos que utiliza esta herramienta para construir hipótesis
sobre diversos factores que determinan la estructura de las relaciones sociales
(en cualquier grupo preseleccionado).
Así mismo, se ha facilitado un manual de uso de algunas aplicaciones
básicas de dos programas de tratamiento informático de datos reticulares, que
nos ayudarán a representar gráficamente las estructuras que pretendemos
analizar y facilitarán nuestra elaboración de hipótesis.
El análisis de redes sociales es un método de análisis científico que
puede ser de gran utilidad para conocer los patrones de relaciones que se
establecen en el interior de una determinada estructura social. Se ha visto
aquí una breve introducción a un método más complejo y sofisticado. Nacido
embrionariamente en los años treinta del siglo XX, y desarrollado profundamente
gracias al impulso de la informática, este método de estudio se ha situado hoy
a la par de otras metodologías utilizadas en ciencias sociales.